CÁLCULO NUMÉRICO

y=3 x=2,1

Pode ser encarado como um caso particular do método do ponto fixo, onde é possível obter uma convergência quadrática. Basta reparar que se f '(z) =/= 0:

f(z) = 0 <=> z = z - f(z) / f '(z)

definindo a função iteradora g(z) = z - f(z) / f '(z), e os pontos fixos de g serão os zeros de f. 
Para além disso, podemos ver que :

g'(z) = f(z) f ''(z) / ( f ' (z) )²

ora como f(z) = 0 então g'(z) = 0 . Pelo teorema anterior, usando esta função iteradora g, é possível arranjar uma vizinhança da raiz onde asseguramos, pelo menos, uma convergência quadrática (desde que f ' (z) =/= 0).

Portanto o método de Newton resume-se a efectuar as iterações:

Historicamente, a origem do método de Newton é geométrica. 
Consiste em definir a nova iterada a partir da intersecção com o eixo das abcissas da tangente à função f (calculada na iterada anterior) :

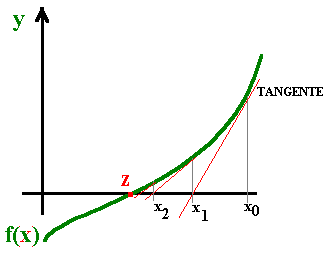
basta reparar que a equação da tangente num ponto x_n é

y = f(x_n ) + f ' (x_n ) ( x - x_n )

e a iterada x_n+1 é a "raiz da tangente", basta pois fazer y = 0 para verificarmos que o valor de x_n+1 coincide com o obtido.

É também claro, mesmo geometricamente, que não podemos ter iteradas em que f ' (x_n) = 0, pois ficariamos com tangentes paralelas ao eixo das abcissas, que nunca o intersectariam (... na "nossa" geometria euclidiana!).