alguém me ajuda a resolver essa questão?

Sendo \(x\) o número de produtos e 10,00 reais o preço do produto, a receita \(R(x)\) é:

\(\Longrightarrow R(x)=10x\)

Sendo \(C(x) = {1 \over 3} x^3 - 6x^2 + 30 x+25\) o custo de produção e \(R(x)=10x\) a receita, o lucro \(L(x)\) é:

\(\Longrightarrow L(x) = R(x)-C(x)\)

\(\Longrightarrow L(x) = (10x)-({1 \over 3} x^3 - 6x^2 + 30 x+25)\)

\(\Longrightarrow L(x) = -{1 \over 3} x^3 + 6x^2 - 20 x-25\)

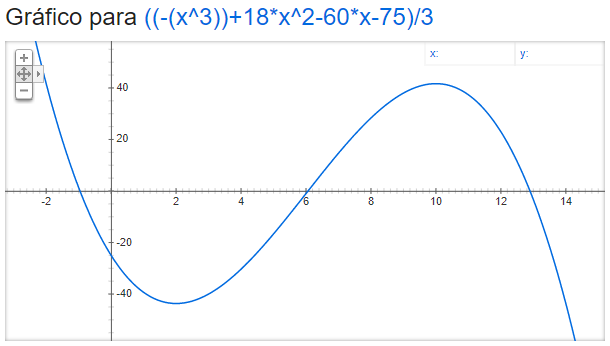
\(\Longrightarrow L(x) = {1 \over 3} (-x^3 + 18x^2 - 60 x-75)\)

O gráfico do lucro \(L(x)\) está apresentado no link a seguir:

Para achar o lucro máximo, deve-se achar o valor de \(x\) que maximiza a função \(L(x)\). Esse valor de \(x\) deve atender à seguinte equação:

\(\Longrightarrow {\partial L(x) \over \partial x } = 0\)

Os valores que atendem à equação anterior são chamados pontos críticos. Pode existir mais de um ponto que atenda à equação anterior.

Dito isso, a equação resultante é:

\(\Longrightarrow {\partial \over \partial x } \Big [ {1 \over 3} (-x^3 + 18x^2 - 60 x-75) \Big ] = 0\)

\(\Longrightarrow {1 \over 3} (-3x^{3-1} + 18\cdot 2x^{2-1} - 60\cdot 1 x^{1-1}-0) = 0\)

\(\Longrightarrow {1 \over 3} (-3x^{2} + 36x - 60) = 0\)

\(\Longrightarrow -x^{2} + 12x - 20 = 0\)

Sendo \(a=-1\), \(b=12\) e \(c=-20\), os pontos críticos são:

\(\Longrightarrow x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)

\(\Longrightarrow x = {-(12) \pm \sqrt{(12)^2-4\cdot (-1) \cdot (-20)} \over 2\cdot (-1)}\)

\(\Longrightarrow x = {-12 \pm \sqrt{144-80} \over -2}\)

\(\Longrightarrow x = {-12 \pm 8 \over -2}\)    \(\to \left \{ \begin{matrix} x_1 = 10 \\ x_2=2 \end{matrix} \right.\)

Um desses pontos críticos é o ponto que maximiza o lucro \(L(x)\).

Agora, vamos encontrar a natureza desses pontos críticos. Para isso, deve ser usada a seguinte equação:

\(\Longrightarrow {\partial ^2 L(x) \over \partial x^2 } = {\partial \over \partial x } (-x^{2} + 12x - 20) \)

\(\Longrightarrow {\partial ^2 L(x) \over \partial x^2 } = -2x^{2-1} + 12\cdot 1x^{1-1} - 0\)

\(\Longrightarrow {\partial ^2 L(x) \over \partial x^2 } =-2x +12\)

Substituindo os pontos críticos, tem-se o seguinte:

\(\Longrightarrow \left \{ \begin{matrix} {\partial ^2 L(x) \over \partial x^2 } \bigg |_{x_1 = 10} =-2x_1 +12 = -2 \cdot 10 + 12 \\ {\partial ^2 L(x) \over \partial x^2 }\bigg |_{x_2 = 2} =-2x_2 +12 = -2 \cdot 2 + 12 \end{matrix} \right.\)   \(\rightarrow \left \{ \begin{matrix} {\partial ^2 L(x) \over \partial x^2 } \bigg |_{x_1 = 10} =-2x_1 +12 = -8<0 \\ {\partial ^2 L(x) \over \partial x^2 }\bigg |_{x_2 = 2} =-2x_2 +12 = 8>0 \end{matrix} \right.\)

Como \({\partial ^2 L(x) \over \partial x^2 } \bigg |_{x_1 = 10}<0\), o ponto crítico \(x_1 = 10\) corresponde a um ponto de máximo.

Como \({\partial ^2 L(x) \over \partial x^2 } \bigg |_{x_2 = 2}>0\), o ponto crítico \(x_2 = 2\) corresponde a um ponto de mínimo.

Portanto, o ponto que maximiza o lucro \(L(x)\) é \(\underline { x_1 = 10 }\).

Finalmente, substituindo \(x_1 = 10\) na função \(L(x)\), o lucro máximo é:

\(\Longrightarrow L_{max} = L(x_1)\)

\(\Longrightarrow L(x) = {1 \over 3} (-x_1^3 + 18x_1^2 - 60 x_1-75)\)

\(\Longrightarrow L(x) = {1 \over 3} \big(-(10)^3 + 18\cdot (10)^2 - 60\cdot (10)-75 \big)\)

\(\Longrightarrow \fbox {$ L(x) = 41,67 \, \mathrm {reais } $}\)