Galera, me ajuda nessa.
Uma chapa de metal plana está disposta em um plano horizontal xy de modo que a temperatura T em (x, y) é dada por T(x, y) = 10(x2 + y2), em que T é expresso em graus e x e y em centímetros. A taxa de variação instantânea de variação T em relação à distância em (1, 2) na direção do eixo x corresponderá a:
|
20 |
||
|
60 |
||
|
14 |
||
|
50 |
||
|
40 |
💡 4 Respostas
Bruno Souza
Quando o exercício diz eixo-x, está querendo dizer na direção u = i (positivo mesmo). Logo, a taxa de variação de T no ponto (1,2) nessa direção será:
dT/du = (dT/dx) i = 10*2*(x²+y²)*2*x = 10*2*(1+4)*2 i = 200 i °C/cm (repare que a unidade é °C/cm, e não cm).
Analogamente, quando o exercício diz eixo-y, temos que a direção será u = j. Assim, temos:
dT/du = (dT/dy) i = 10*2*(x²+y²)*2*y = 10*2*(1+4)*4 i = 400 j °C/cm
Já para o último caso, primeiro temos que normalizar o vetor a:
u = a/||a|| = (2/√5)i + (1/√5)j
Já sabemos os valores das derivadas parciais de T em y e x no ponto (1,2)
dT/dx = 200 °C/cm
dT/dy = 400 °C/cm
Assim temos que
dT/du = (dT/dx)*(2/√5)i + (dT/dy)*(1/√5)j °C/cm
dT/du = (400/√5)i + (400/√5)j °C/cm
Andre Smaira
Contextualização:
Se y é uma função de x, e n é um inteiro positivo, então uma relação de igualdade (que não se reduz a uma identidade) que envolva x, y, y', y'', ...,y(n) é chamada uma equação diferencial de ordem n.
Equação diferencial é uma equação que apresenta derivadas ou diferenciais de uma função desconhecida (a incógnita da equação).
Classificação
Equação Diferencial Ordinária (EDO): Envolve derivadas de uma função de uma só variável independente.
Equação Diferencial Parcial (EDP): Envolve derivadas parciais de uma função de mais de uma variável independente.
Ordem: é a ordem da derivada de mais alta ordem da função incógnita que figura na equação.
Exemplos:

, tem ordem 1 e grau 1
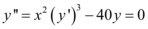
, tem ordem 2 e grau 3
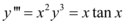
, tem ordem 3 e grau 3
Referência: https://www.somatematica.com.br/superior/equacoesdif/eq.php - Acessado em 12/10/2018
Resolução:
Para calcularmos a taxa de variação instantânea de T em relação à distância na direção do eixo x, devemos derivar a função 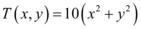 em função da variável x, conforme abaixo:
em função da variável x, conforme abaixo:
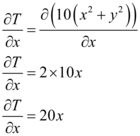
Sendo assim, no ponto (1,2), a taxa de variação instantânea de T em relação à distância na direção do eixo x é:
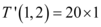
Portanto:
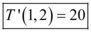
Conclusão:
Portanto, no ponto (1,2), a taxa de variação instantânea de T em relação à distância na direção do eixo x é:
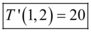
Andre Smaira
Contextualização:
Se y é uma função de x, e n é um inteiro positivo, então uma relação de igualdade (que não se reduz a uma identidade) que envolva x, y, y', y'', ...,y(n) é chamada uma equação diferencial de ordem n.
Equação diferencial é uma equação que apresenta derivadas ou diferenciais de uma função desconhecida (a incógnita da equação).
Classificação
Equação Diferencial Ordinária (EDO): Envolve derivadas de uma função de uma só variável independente.
Equação Diferencial Parcial (EDP): Envolve derivadas parciais de uma função de mais de uma variável independente.
Ordem: é a ordem da derivada de mais alta ordem da função incógnita que figura na equação.
Exemplos:
, tem ordem 1 e grau 1
, tem ordem 2 e grau 3
, tem ordem 3 e grau 3
Referência: https://www.somatematica.com.br/superior/equacoesdif/eq.php - Acessado em 12/10/2018
Resolução:
Para calcularmos a taxa de variação instantânea de T em relação à distância na direção do eixo x, devemos derivar a função em função da variável x, conforme abaixo:
Sendo assim, no ponto (1,2), a taxa de variação instantânea de T em relação à distância na direção do eixo x é:
Portanto:
Conclusão:
Portanto, no ponto (1,2), a taxa de variação instantânea de T em relação à distância na direção do eixo x é:
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Compartilhar