Qual A fórmula para cálculo de juros compostos?

O regime de juros compostos é o mais comum no sistema financeiro, sendo portanto o mais útil para cálculos de problemas do dia a dia. Os juros gerados a cada período são incorporados ao principal para o cálculo dos juros do período seguinte.

Chamamos de capitalização o momento em que os juros são incorporados ao principal.

Após três meses de capitalização, temos:

1º mês: M =P.(1 + i)
2º mês: o principal é igual ao montante do mês anterior: M = P.(1 + i).(1 + i) 
3º mês: o principal é igual ao montante do mês anterior: M = P.(1 + i).(1 + i).(1 + i)

Simplificando, obtemos a fórmula:

Importante: a taxa i tem que ser expressa na mesma medida de tempo de n, ou seja, taxa de juros ao mês para n meses.

Para calcularmos apenas os juros, basta diminuir o principal do montante ao final do período:

Exemplo:

Calcule o montante de um capital de R$ 6.000,00, aplicado a juros compostos, durante 1 ano, à taxa de 3,5% ao mês. (use log 1,035=0,0149 e log 1,509=0,1788)

Resolução:

P = R$6.000,00
t = 1 ano = 12 meses
i = 3,5 % a.m. = 0,035
M = ?

Usando a fórmula M=P.(1+i)ⁿ, obtemos:

M  =  6000.(1+0,035)¹²  =  6000. (1,035)¹² = 9066,41

Portanto o montante é R$ 9.066,41.

Contextualização:

Juros compostos são a aplicação de juros sobre juros, isto é, os juros compostos são aplicados ao montante de cada período.

Juros compostos são muito utilizados pelo sistema financeiro, pois oferece uma rentabilidade melhor. A taxa de juros é sempre aplicada ao somatório do capital no final de cada mês.

Algumas características do Juros Compostos:

• Os juros compostos rendem somente no vencimento da aplicação;
• Os rendimentos por juros compostos tem crescimento ascendente, isto é, a cada mês os juros são calculados em cima do capital mais os rendimentos anteriores; isto faz com que os juros do mês seguinte seja maior que o do mês anterior.
• Tem crescimento exponencial, cresce muito mais rápido, formando uma curva ascendente.

Para entender melhor veja com fica o montante da aplicação mês a mês com juros compostos:

Primeiro mês:

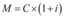
Segundo mês:

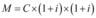
Terceiro mês:

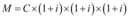
E assim por diante. Para cada mês os juros são calculados em cima do capital inicial C mais os juros mês a mês. Esse tipo de remuneração em juros compostos com o passar do tempo tende a ser muito rentável, já que ele tem um crescimento exponencial.

Resolução:

Fórmula para calcular o Montante em juros compostos:

Para simplificar, obtemos a fórmula a seguir que representa o montante, ou seja, o valor final com o capital mais os juros aplicados:

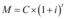
Onde:

M é o montante final obtido na aplicação, ou seja, o saldo após a aplicação dos juros;

i é a taxa de juros aplicada, em porcentagem;

C é o capital ou valor inicial aplicado;

t é o tempo total da aplicação.

A taxa de juros i deve ser escrita na forma decimal. Para transformar um número em decimal, divida ele por 100, pois a taxa é em porcentagem.

Fórmula para calcular juros compostos:

O cálculo somente dos juros, ou seja, o rendimento que a aplicação obteve, é obtido pela seguinte fórmula:

Onde:

J são os juros;

M é o montante que pode ser calculado pela fórmula do montante acima;

C é o capital ou valor inicial aplicado.

Conclusão:

Sendo assim, o cálculo somente dos juros, que é o rendimento que a aplicação obteve, é obtido pela seguinte fórmula:

Importante:

Quando aplicarmos esta fórmula, devemos ficar atentos às seguintes regras:

- se a taxa i for ao ano, o tempo t deve ser reduzido à unidade de ano;

- se a taxa i for ao mês, o tempo t deve ser reduzido à unidade de mês;

- se a taxa i for ao dia, o tempo t deve ser reduzido à unidade de dia.