SISTEMAS DE CONTROLE I
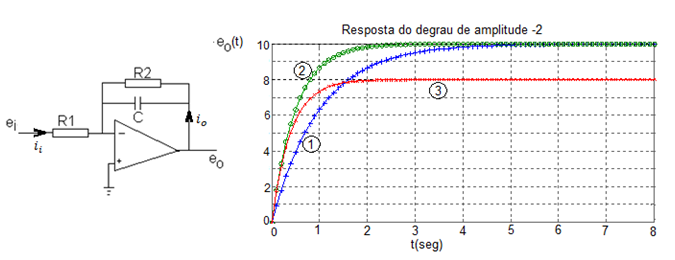
A figura abaixo apresenta um sistema de primeira ordem, construído a partir de um amplificador operacional, sendo eia tensão de entrada e eo a tensão de saída.
No gráfico, são apresentadas três respostas ao degrau de amplitude -2, sendo que em todas elas foi utilizado o mesmo valor de R1.
Pede-se:
a) Determine a equação diferencial padrão de 1a. ordem para representar o sistema, em função de R1, R2 e C.
b) Determine a função de transferência do sistema, seu ganho e constante de tempor, em função de R1, R2 e C.
c) Com R1=1kΩ, determine os valores R2 e C para as respostas 1, 2 e 3.
💡 5 Respostas
Andre Smaira
Para determinar a equação diferencial que representa o sistema, vamos utilizar o fato de que as tensões \({V_ + }\) e \({V_ - }\) nas entradas não-inversora e inversora do amplificador operacional são iguais quando o seu ganho é infinito.
---
Como a entrada não-inversora está aterrada, conclui-se que\({V_ + } = 0\). Logo, devemos ter \({V_ - } = 0\). Assim, analisar o circuito abaixo, onde :

Autoria Própria
---
Pela lei de Ohm, podemos calcular as correntes \({i_i}\) e \({i_{R2}}\), obtendo \({i_i} = \dfrac{{{e_i}}}{{R1}}\) e \({i_{R2}} = -\dfrac{{{e_0}}}{{R2}}\). Temos, ainda, que \({i_C} = C\dfrac{{d{v_c}}}{{dt}}\). Aplicando a lei dos nós ao nó da entrada inversora, temos:
\[\eqalign{ {i_i} &= {i_{R2}} + {i_C}\cr\dfrac{{{e_i}}}{{R1}} &= - \dfrac{{{e_0}}}{{R2}} + C\dfrac{{d{v_c}}}{{dt}}\cr\dfrac{{R2}}{{R1}}{e_i} &= - {e_o} + R2 \cdot C\dfrac{{d{v_c}}}{{dt}} }\]
---
Como \({v_C} = {e_o}\), podemos escrever:
\[\eqalign{ \dfrac{{R2}}{{R1}}{e_i}\left( t \right) &= - {e_o}\left( t \right) + R2 \cdot C\dfrac{{d{e_o}\left( t \right)}}{{dt}}\cr- {e_o}\left( t \right) + R2 \cdot C\dfrac{{d{e_o}\left( t \right)}}{{dt}} &= \dfrac{{R2}}{{R1}}{e_i}\left( t \right) }\]
---
Portanto, a equação diferencial de 1ª ordem do sistema é \(\boxed{ - {e_o}\left( t \right) + R2 \cdot C\dfrac{{d{e_o}\left( t \right)}}{{dt}} = \dfrac{{R2}}{{R1}}{e_i}\left( t \right)}\).
---
b)
A função de transferência \(G\left( s \right)\), no domínio de Laplace, que relaciona a entrada \({{E_i}\left( s \right)}\) e a saída \({{E_o}\left( s \right)}\). Matematicamente, temos:
\[G\left( s \right) = \dfrac{{{E_o}\left( s \right)}}{{{E_i}\left( s \right)}}\]
---
Vamos aplicar a transformada de Laplace em ambos os membros da equação diferencial encontrada. Como a transformada de Laplace da derivada é \(\mathcal{L}\left( {\dfrac{{dx\left( t \right)}}{{dt}}} \right) = s \cdot X\left( s \right)\), temos:
\[\eqalign{ \mathcal{L}\left( { - {e_o}\left( t \right) + R2 \cdot C\dfrac{{d{e_o}\left( t \right)}}{{dt}}} \right) &= \mathcal{L}\left( {\dfrac{{R2}}{{R1}}{e_i}\left( t \right)} \right)\cr- {E_o}\left( s \right) + R2 \cdot C \cdot s \cdot {E_o}\left( s \right) &= \dfrac{{R2}}{{R1}}{E_i}\left( s \right)\cr\left( {s \cdot R2 \cdot C - 1} \right){E_o}\left( s \right) &= \dfrac{{R2}}{{R1}}{E_i}\left( s \right)\cr\dfrac{{{E_o}\left( s \right)}}{{{E_i}\left( s \right)}} &= \dfrac{{R2}}{{R1}} \cdot \dfrac{1}{{\left( {s \cdot R2 \cdot C - 1} \right)}} }\]
---
Logo, a função de transferência é \(G\left( s \right) = \dfrac{{R2}}{{R1}} \cdot \dfrac{1}{{\left( {s \cdot R2 \cdot C - 1} \right)}}\). Para o ganho do sistema, devemos calcular o módulo da função de transferência. Assim:
\[\eqalign{ \left| {G\left( s \right)} \right| &= \left| {\dfrac{{R2}}{{R1}} \cdot \dfrac{1}{{\left( {s \cdot R2 \cdot C - 1} \right)}}} \right|\cr&= \dfrac{{R2}}{{R1}} \cdot \left| {\dfrac{1}{{\left( {s \cdot R2 \cdot C - 1} \right)}}} \right|\cr&= \dfrac{{R2}}{{R1}} \cdot \dfrac{1}{{\sqrt {1 + {{\left( {R2 \cdot C} \right)}^2}} }} }\]
---
Para a constante de tempo \(\tau\), devemos escrever a equação diferencial do sistema na forma \(\tau \dfrac{{d{e_o}}}{{dt}} + {e_0}\left( t \right) = {e_i}\left( t \right)\). Da equação diferencial encontrada, temos que \(\tau = R2 \cdot C\).
---
Portanto, temos que \(\boxed{G\left( s \right) = \dfrac{{R2}}{{R1}} \cdot \dfrac{1}{{\left( {s \cdot R2 \cdot C - 1} \right)}}}\), \(\boxed{\left| {G\left( s \right)} \right| = \dfrac{{R2}}{{R1}} \cdot \dfrac{1}{{\sqrt {1 + {{\left( {R2 \cdot C} \right)}^2}} }}}\) e \(\boxed{\tau = R2 \cdot C}\).
---
c)
Para a resposta 1, do gráfico, temos que \({e_o}\left( 5 \right) = 10\). Como a entrada é um degrau de amplitude -2 o ganho , em módulo, é igual a 5. Com \(R1 = 1{\text{ k}}\Omega\), substituindo na fórmula do ganho, temos \(R2 = 5{\text{ k}}\Omega\) e \(C = 200 \cdot {10^{ - 6}}{\text{ F}}\).
---
Analogamente, para a resposta 2, temos \({e_o}\left( 1 \right) = 6\). Logo, o módulo do ganho é igual a 3. Substituindo na fórmula, temos \(R2 = 5{\text{ k}}\Omega\) e .\(C = 100 \cdot {10^{ - 6}}{\text{ F}}\)
---
E, para a resposta 3, temos \({e_o}\left( 2 \right) = 8\). Logo, o módulo do ganho é igual a 4. Substituindo na fórmula, temos \(R2 = 5{\text{ k}}\Omega\) e \(C = 250 \cdot {10^{ - 6}}{\text{ F}}\).
---
Portanto, para as respostas 1, 2 e 3, as capacitâncias são de \(\boxed{C = 200 \cdot {{10}^{ - 6}}{\text{ F}}}\), \(\boxed{C = 100 \cdot {{10}^{ - 6}}{\text{ F}}}\) e \(\boxed{C = 250 \cdot {{10}^{ - 6}}{\text{ F}}}\), respectivamente. Para a resistência, temos para as três respostas o valor \(\boxed{R2 = 5{\text{ k}}\Omega }\).
Wesley Carvalho
NAO SEI BRO
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas dessa disciplina
Conteúdos escolhidos para você
 125 pág.
125 pág. 18 pág.
18 pág.




Compartilhar