Ache o valor de X?

---

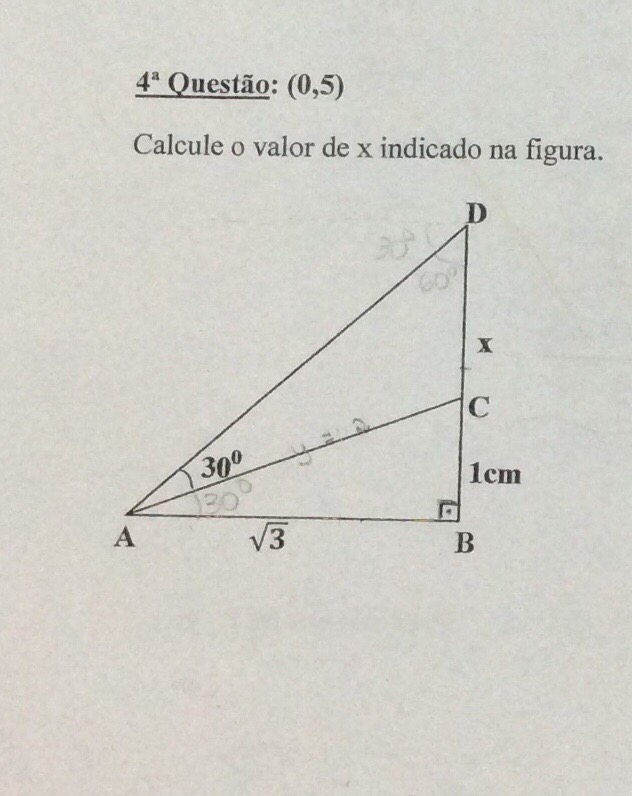
Pelo Teorema de Pitágoras, temos que \(AC=\sqrt{AB^2+BC^2}=\sqrt{\sqrt{3}^2+1^2}=\sqrt4=2\). O ângulo \(BAC\) é o ângulo cuja a tangente vale \(\dfrac{BC}{AB}\), então \(BAC=arctg\dfrac{1}{\sqrt3}=30°\). Portanto, o ângulo \(DAB\) vale \(60°\). Usando as relações trigonométricas, podemos calcular o tamanho do segmento \(AD\), pois \(cos\,60°=\dfrac{AB}{AD}=\dfrac{1}2\). Assim, temos \(AD=2AB=2{\sqrt3}\). Novamente, pelo Teorema de Pitágoras, temos \(AD^2=AB^2+BD^2\). Podemos então calcular o tamanho do segmento \(BD\): \(BD=\sqrt{AD^2-AB^2}=\sqrt{(2\sqrt{3})^2-\sqrt3^2}=\sqrt{9}=3\). Finalmente, podemos calcular \(x\), pois \(x=BD-BC=3-1=2\).

----

Portanto, temos que \(\boxed{x=2\,cm}\).