um determinado triângulo retângulo ABC com angulo reto na vértice A tem =6cm ,Ac =6√3 bc =12cm calcule os valores dos ângulos​

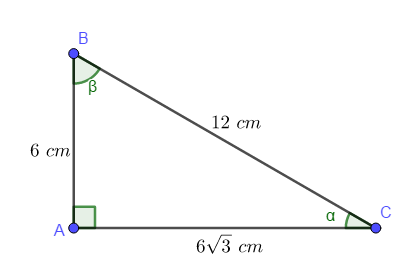
Os ângulos são facilmente encontrados usando a trigonometria.

\(sen(\alpha)=\dfrac{Cat. Oposto}{hip.}\rightarrow sen(\alpha)=\dfrac{6}{12}=\dfrac{1}{2}\rightarrow \alpha=30º\)

Sabendo que o ângulo \(\alpha\) é de 30 graus, então o ângulo \(\beta\) sai de graça. Pois a soma dos ângulos internos de um triângulo é de 180 graus. Logo:

\(\alpha+\beta+90=180\rightarrow\beta=180-90-30\rightarrow\beta=60\)

Cateto oposto ao ângulo y: AC

Cateto adjacente ao ângulo x: AC

Hipotenusa: BC

Assim, para descobrir os ângulos x e y, vamos utilizar as seguintes relações geométricas:

\[sen(y)=\dfrac{AC}{BC}\\cos (x)=\dfrac{AC}{BC}\\\]
Substituindo os valores:$$sen(y)=\dfrac{6\sqrt3}{12}=\dfrac{\sqrt3}2

\\cos (x)=\dfrac{6\sqrt3}{12}=\dfrac{\sqrt3}2\\

\[Utilizando o arcsen e arcos:\]
y=arcsen(\dfrac{\sqrt3}2)=60º\\

x=arcos(\dfrac{\sqrt3}2)=30º

\[Portanto, os ângulos desse triângulo retângulo são \]
\boxed{30º}\:\: \boxed{60º}

$$