Alguém pode me ajudar com esse exercício??

\[\eqalign{h&=\dfrac{a\sqrt3}2\cr 6&=\dfrac{a\sqrt3}2\cr a&=\dfrac{12}{\sqrt3}}\]

Racionalizando o denominador ao multiplicarmos por \(\sqrt3\) temos:

\[a=\dfrac{12\sqrt3}3=4\sqrt3\ cm\]

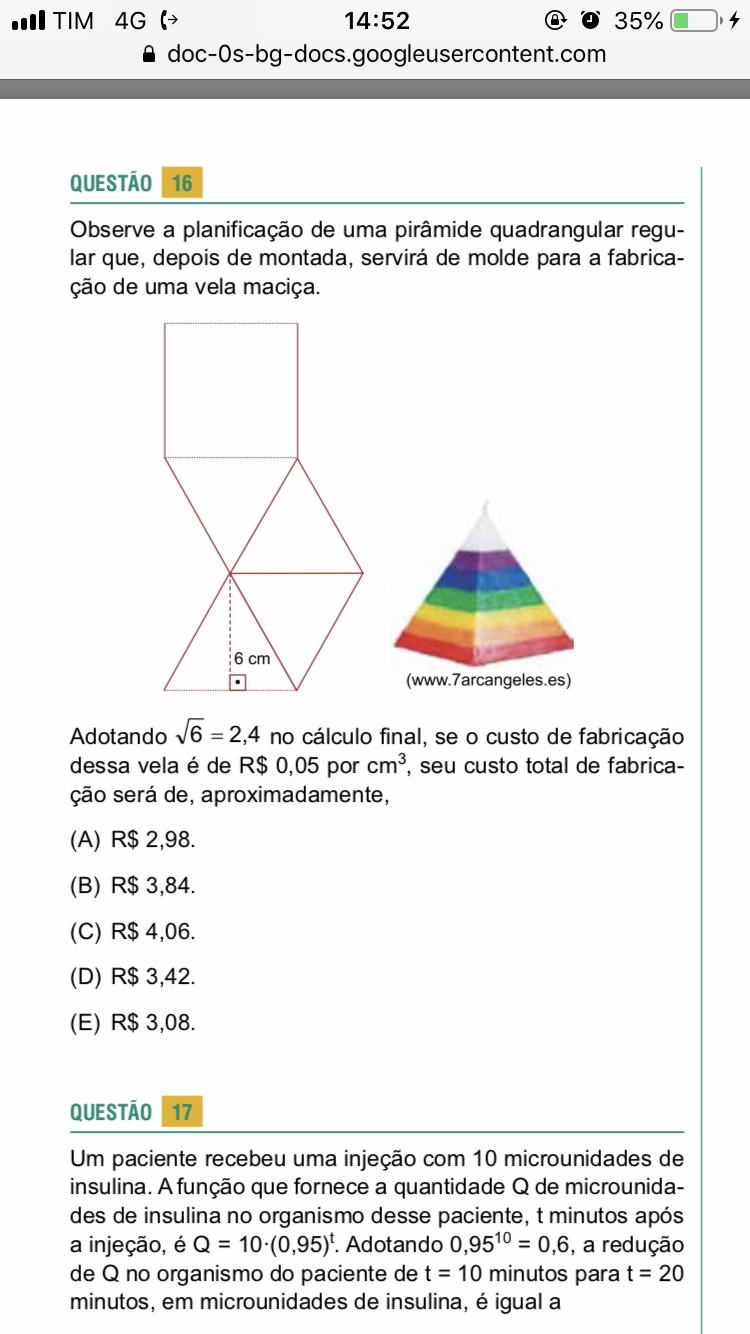
Para determinarmos a altura da pirâmide vamos usar o Teorema de Pitágoras em um triângulo retângulo cujos catetos são a altura da pirâmide e metade da aresta e a hipotenusa é a altura da face triangular:

\[H^2+(a/2)^2=h^2\]

\[H^2+(2\sqrt3)^2=6^2\]

\[H^2+4\cdot3=36\]

\[H^2=36-12=24\Rightarrow H=\sqrt{4\cdot6}=2\sqrt6\ cm\]

Para o volume de uma pirâmide, temos:

\[V=\dfrac13A_bH\]

Para nosso caso a base é um quadrado:

\[V=\dfrac13a^2H=\dfrac13\cdot(4\sqrt3)^2\cdot(2\sqrt6)=\dfrac1{\require{cancel}\cancel3}\cdot(16\cdot\require{cancel}\cancel3)\cdot(2\sqrt6)=32\sqrt6\ cm^3\]

Mas o valor da unidade de volume é \(R$\ 0,05\) de forma que:

\[C=0,05V=\dfrac{V}{20}=\dfrac{32}{20}\sqrt6=\dfrac85\sqrt6\]

O enunciado diz que consideremos \(\sqrt6=2,4\):

\[C=\dfrac85\cdot2,4=\dfrac{19,2}5\]

Logo:

\[\boxed{C=R$\ 3,84}\]

O que nos leva à alternativa B.