qual o calculo para curto circuito bifasico a terra?

\[T= \begin{bmatrix} 1 & 1 & 1 \\ 1 & \alpha^2 & \alpha \\ 1 & \alpha & \alpha^2 \\ \end{bmatrix}, \,\,\, \alpha=1 \angle 120^{\circ}\]

Portanto, a inversa de \(T\)é:

\[T^{-1}= {1 \over 3}\begin{bmatrix} 1 & 1 & 1 \\ 1 & \alpha & \alpha^2 \\ 1 & \alpha^2 & \alpha \\ \end{bmatrix}, \,\,\, \alpha=1 \angle 120^{\circ}\]

Com isso, a relação entre as correntes na sequência abc e as correntes na sequência 012 é:

\[\begin{bmatrix} I_{a0} \\ I_{a1} \\I_{a2} \end{bmatrix} = T^{-1} \cdot \begin{bmatrix} I_a \\ I_b \\I_c \end{bmatrix} \,\,\,\, (I)\]

Analogamente para a tensão:

\[\begin{bmatrix} V_{a0} \\ V_{a1} \\V_{a2} \end{bmatrix} = T^{-1} \cdot \begin{bmatrix} V_a \\ V_b \\V_c \end{bmatrix} \,\,\,\, (II)\]

Supondo que o curto circuito bifásico à terra envolve as fases b e c em um gerador (de tensão \(E\)) operando sem carga, tem-se a seguinte representação:

\

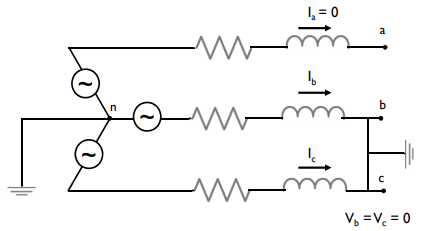
Com \(V_b=V_c=0\) a equação matricial \((II)\)fica da seguinte forma:

\[\begin{bmatrix} V_{a0} \\ V_{a1} \\V_{a2} \end{bmatrix} = T^{-1} \cdot \begin{bmatrix} V_a \\ V_b \\V_c \end{bmatrix} \\ \begin{bmatrix} V_{a0} \\ V_{a1} \\V_{a2} \end{bmatrix} = {1 \over 3}\begin{bmatrix} 1 & 1 & 1 \\ 1 & \alpha & \alpha^2 \\ 1 & \alpha^2 & \alpha \\ \end{bmatrix} \cdot \begin{bmatrix} V_a \\ 0 \\ 0 \end{bmatrix}\]

Portanto, a solução da equação matricial é:

\[V_{a0}=V_{a1}=V_{a2}={V_a \over 3} \,\,\,\, (III)\]

De acordo com o esquema abc mostrado, tem-se a seguinte equação matricial:

\[\begin{bmatrix} V_{a} \\ V_{b} \\V_{c} \end{bmatrix} = \begin{bmatrix} E \\ E \\ E \end{bmatrix} - \begin{bmatrix} Z_a & 0 & 0 \\ 0 & Z_b & 0 \\ 0 & 0 & Z_c \end{bmatrix}\cdot \begin{bmatrix} I_a \\ I_b \\I_c \end{bmatrix}\]

Onde \(Z_a\) \(Z_b\)e \(Z_c\)são as impedâncias da sequência abc.

Realizando manipulações matemáticas, tem-se o seguinte:

\[g\{T \cdot \begin{bmatrix} V_{a0} \\ V_{a1} \\V_{a2} \end{bmatrix}g\} = \begin{bmatrix} E \\ E \\ E \end{bmatrix} - \begin{bmatrix} Z_a & 0 & 0 \\ 0 & Z_b & 0 \\ 0 & 0 & Z_c \end{bmatrix}\cdot g\{T \cdot \begin{bmatrix} I_{a0} \\ I_{a1} \\I_{a2} \end{bmatrix} \bigg\}\]

Multiplicando os dois lados da equação por \(T^{-1}\) tem-se o seguinte:

\[\begin{bmatrix} V_{a0} \\ V_{a1} \\V_{a2} \end{bmatrix} = T^{-1} \cdot \begin{bmatrix} E \\ E \\ E \end{bmatrix} - g\{T^{-1} \cdot\begin{bmatrix} Z_a & 0 & 0 \\ 0 & Z_b & 0 \\ 0 & 0 & Z_c \end{bmatrix}\cdot T g\}\cdot \begin{bmatrix} I_{a0} \\ I_{a1} \\I_{a2} \end{bmatrix} \\ \begin{bmatrix} V_{a0} \\ V_{a1} \\V_{a2} \end{bmatrix} = \begin{bmatrix} 0 \\ E_a \\ 0 \end{bmatrix} - \begin{bmatrix} Z_0 & 0 & 0 \\ 0 & Z_1 & 0 \\ 0 & 0 & Z_2 \end{bmatrix}\cdot \begin{bmatrix} I_{a0} \\ I_{a1} \\I_{a2} \end{bmatrix} \,\,\,\,(IV)\]

Onde \(Z_0\) \(Z_1\)e \(Z_2\)são as impedâncias da sequência 012.

Unindo as equações \((III)\)e \((IV)\) a representação fica da seguinte forma:

\

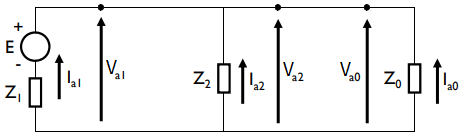
Pela nova representação na sequência 012, tem-se a seguinte equação:

\[I_{a1}={E_a \over Z_1 + {Z_0\cdot Z_2\over Z_0+Z_2}}\]

Resumidamente, o cálculo para curto circuito bifásico à terra é realizado com base nas seguintes equações:

\[\boxed{\left\{ \begin{matrix} \eqalign{ I_a=I_{a0}+I_{a1}+I_{a2}&=0 \cr V_{a0}=V_{a1}=V_{a2}&={V_a \over 3} \\ I_{a1}&={E_a \over Z_1 + {Z_0\cdot Z_2\over Z_0+Z_2}} } \end{matrix} \right.}\]