Um arqueiro, durante uma competição de arco e flecha, puxa seu arco fabricado em plástico reforçado com Kevlar 49 até este ter um raio de 12 metros, e solta a flecha. Sabendo-se que o perfil deste arco pode ser aproximado como retangular, com 10 mm de espessura e 40 mm de largura, determine a tensão de flexão máxima do arco.

Question

Um arqueiro, durante uma competição de arco e flecha, puxa seu arco fabricado em plástico reforçado com Kevlar 49 até este ter um raio de 12 metros...

Ed · Answer

Para determinar a tensão de flexão máxima do arco, precisamos usar a fórmula da tensão de flexão:

$$
\sigma = \frac{M \cdot c}{I}
$$

onde:
- $\sigma$ é a tensão de flexão,
- $M$ é o momento fletor,
- $c$ é a distância do eixo neutro até a fibra mais distante,
- $I$ é o momento de inércia da seção transversal.

1. **Cálculo do momento de inércia $I$**:
   Para uma seção retangular, o momento de inércia é dado por:

$$
   I = \frac{b \cdot h^3}{12}
   $$

onde $b$ é a largura e $h$ é a altura. Neste caso, a largura $b = 40 \, \text{mm} = 0,04 \, \text{m}$ e a altura $h = 10 \, \text{mm} = 0,01 \, \text{m}$.

$$
   I = \frac{0,04 \cdot (0,01)^3}{12} = \frac{0,04 \cdot 0,000001}{12} = \frac{0,00000004}{12} \approx 3,33 \times 10^{-9} \, \text{m}^4
   $$

2. **Cálculo da distância $c$**:
   A distância do eixo neutro até a fibra mais distante (metade da altura):

$$
   c = \frac{h}{2} = \frac{0,01}{2} = 0,005 \, \text{m}
   $$

3. **Cálculo do momento fletor $M$**:
   O momento fletor pode ser calculado considerando a força aplicada e a distância. Para um arco, isso pode ser mais complexo, mas se considerarmos uma força $F$ aplicada no centro do arco, o momento fletor pode ser estimado. Para simplificar, vamos assumir que a força é a força de tração no arco.

Se não temos a força, não podemos calcular $M$ diretamente. Precisaríamos de mais informações sobre a força aplicada.

4. **Cálculo da tensão de flexão $\sigma$**:
   Com $M$ conhecido, podemos substituir na fórmula da tensão de flexão.

Como não temos a força aplicada, não podemos calcular a tensão de flexão máxima sem essa informação. Se você tiver a força ou mais detalhes sobre a situação, posso ajudar a calcular a tensão.

Ed · Answer

Para determinar a tensão de flexão máxima do arco, precisamos utilizar a fórmula da tensão de flexão:

σ = (M * c) / (I * y)

Onde:
σ é a tensão de flexão máxima
M é o momento fletor
c é a distância do centroide à fibra mais distante
I é o momento de inércia da seção transversal
y é a distância da fibra mais distante ao eixo neutro

No caso do arco retangular, o momento de inércia (I) é dado por:

I = (b * h^3) / 12

Onde:
b é a largura da seção transversal
h é a espessura da seção transversal

Substituindo os valores fornecidos:
b = 40 mm = 0,04 m
h = 10 mm = 0,01 m

Calculando o momento de inércia:
I = (0,04 * 0,01^3) / 12 = 3,33 x 10^-8 m^4

Agora, precisamos determinar o momento fletor (M). Para isso, podemos utilizar a relação entre o momento fletor e a tensão de flexão máxima:

M = σ * I * y / c

Sabendo que o raio do arco é de 12 metros, podemos considerar que a distância do centroide à fibra mais distante (c) é igual a metade do raio:

c = 12 m / 2 = 6 m

Assumindo que a flecha é lançada no ponto mais distante do arco, a distância da fibra mais distante ao eixo neutro (y) é igual à metade da espessura:

y = 10 mm / 2 = 5 mm = 0,005 m

Agora, podemos calcular o momento fletor:
M = σ * I * y / c

Substituindo os valores:
M = σ * (3,33 x 10^-8 m^4) * (0,005 m) / (6 m)

A tensão de flexão máxima (σ) não foi fornecida na pergunta, portanto, não é possível determinar o valor exato da tensão de flexão máxima do arco.

Ícaro Ramos · Answer

546 MPa﻿Resposta correta. A alternativa está correta, para resolução deste problema, só precisamos do valor tabelado do módulo de elasticidade para o material, de posse deste valor e substituindo a relação de momento-curvatura na fórmula da tensão de flexão, ficamos com a relação onde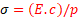, sendo c metade da espessura da viga e p o raio de flexão da viga, de posse dos dados só é necessário substituir os valores na fórmula.

Resistência dos Materiais

A4 - Resistência dos materiais

Respostas

Crie sua conta grátis para liberar essa resposta. 🤩

Ainda com dúvidas?

Essa pergunta também está no material:

A4 - Resistência dos materiais

Mais conteúdos dessa disciplina