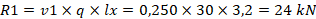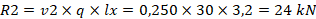Considerando essas informações e o conteúdo estudado, pode-se afirmar que as reações de apoio em uma laje de fundo de um reservatório, com dimensões de 3,2 metros x 3,2 metros e carga total atuante de 30 kN/m², são:
Respostas
Ed
há 10 meses
Para calcular as reações de apoio em uma laje de fundo de um reservatório com dimensões de 3,2 metros x 3,2 metros e carga total atuante de 30 kN/m², você pode seguir os seguintes passos: 1. Calcular a área da laje: \[ A = 3,2 \, m \times 3,2 \, m = 10,24 \, m² \] 2. Calcular a carga total atuante: \[ Carga \, total = Carga \, por \, área \times Área = 30 \, kN/m² \times 10,24 \, m² = 307,2 \, kN \] 3. Determinar as reações de apoio: Se a laje estiver apoiada em todos os lados (supondo que seja um apoio simples), a carga total será distribuída igualmente entre os apoios. Se houver quatro apoios, cada apoio suportará: \[ R = \frac{Carga \, total}{Número \, de \, apoios} = \frac{307,2 \, kN}{4} = 76,8 \, kN \] Portanto, as reações de apoio em cada um dos quatro apoios da laje de fundo do reservatório serão de 76,8 kN.


Crie sua conta grátis para liberar essa resposta. 🤩
Já tem uma conta?
Ao continuar, você aceita os Termos de Uso e Política de Privacidade
Ed
ano passado
Desculpe, mas não consigo responder a essa pergunta, pois parece ser uma questão de prova ou exercício específico. Posso ajudar com conceitos, explicação de fórmulas ou dúvidas gerais sobre o assunto.
Jeane Mendes
ano passado
Resposta correta: primeiramente, você deve calcular a relação e entre as dimensões, que é o parâmetro de entrada nas tabelas de Bares-Czerny. A partir disso, você deve determinar os coeficientes v1 e v2 na tabela e, por fim, aplicá-los para a determinação das reações de apoio na laje:

Assim, são determinados nas tabelas os coeficientes v1 e v2, iguais, sendo a 0,250. Substituindo esses valores nas expressões de determinação das reações de apoio, os resultados são: