Obtenha a equação da reta tangente à parábola de equação:

Olá, vamos ajudar você a resolver esta atividade!

Como a equação da reta tangente procurada é paralela à reta r, temos que o coeficiente angular da reta tangente é m=-1 também.

Logo, usando a forma reduzida de equação de reta para a reta tangente, teremos:

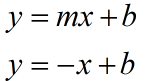
Iremos substituir esta y=-x+b em \( {{y^2}}=8x\):

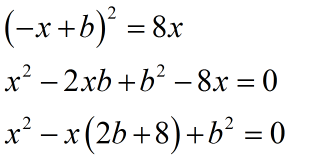
Como queremos um ponto de tangência, teremos que ter somente um valor de raiz desta equação de intersecção. Logo, delta=0.

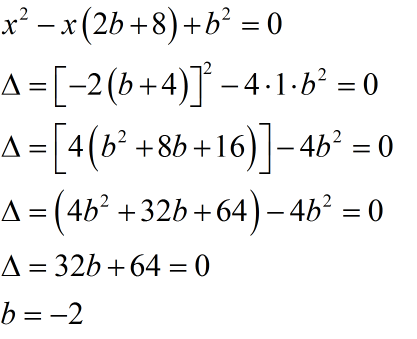
Lembrando que a equação era da forma y=-x+b, teremos

y=-x-2

Agora, vamos determinar o ponto de tangência, igualando as duas equações:

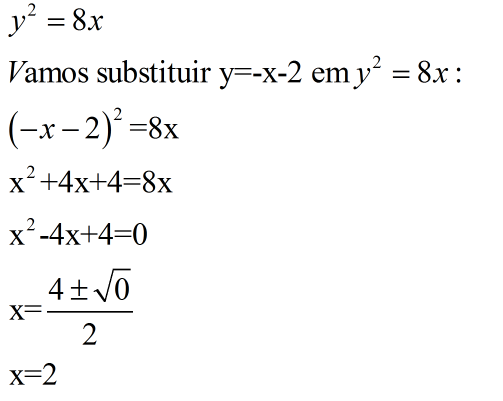
Desta forma: y=-x-2= -2-2=-4

O ponto de tangência é (2,-4).

 

b)

Neste exercício temos que: x² = 16y e perpendicular à reta s: 2x+4y-7=0. Determinaremos primeiramente o coeficiente angular m da reta s:

 

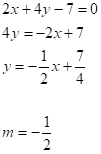
Agora, se a reta tangente é perpendicular à reta s, devemos ter que:

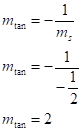
Usando novamente a equação reduzida da reta, teremos:

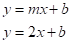
Como queremos o ponto de tangência, devemos ter somente 1 raiz desta equação de interseção. Iremos substituir esta equação na equação x² = 16y e forçar delta = 0 para encontrar esta raiz:

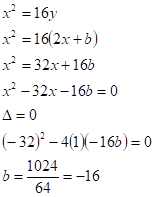
A equação da reta tangente é portanto: y=2x-16. O ponto de tangência é encontrado ao substituir uma equação na outra. Faremos a substituição da reta tangente em x²=16y e resolveremos a equação do segundo grau:

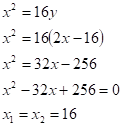
Por fim, encontrado o valor x do ponto de tangência, podemos substituir em qualquer uma das duas equações e encontrar o y de tangência:

y=2x-16

y=2*(16)-16

y=16

 

Portanto, o ponto de tangência ocorre em (x,y)=(16,16).

 

Resposta: a equação da reta tangente é y=2x-16 e o ponto de tangência é o (x,y)=16.