Como calcular essa soma 1^2 + 2^2 + 3^2 + ... + (n-1)^2 +n^2

Boa noite!

Vamos desenvolver uma soma antes:

(0+1)^2=0^2+2(0)(1)+1^2

(1+1)^2=1^2+2(1)(1)+1^2

(2+1)^2=2^2+2(2)(1)+1^2

....

(n+1)^2=n^2+2(n)(1)+1^2

Somando do lado esquerdo e do lado direito temos, após cancelar os termos iguais:

(n+1)^2=2(1+2+3+...+n)+(n+1)

(n+1)^2=2(Sn)+(n+1)

2Sn=(n+1)^2-(n+1)=(n+1)(n+1-1)=(n+1)n

Sn=n(n+1)/2

Chegamos na fórmula da soma dos n primeiros inteiros (de 1 a n)

Podemos utilizar este mesmo raciocínio para obter a fórmula em questão, mas, agora, usando (n+1)^3

Então:

(0+1)^3=0^3+3(0)^2(1)+3(0)(1)^2+1^3

(1+1)^3=1^3+3(1)^2(1)+3(1)(1)^2+1^3

(2+1)^3=2^3+3(2)^2(1)+3(2)(1)^2+1^3

...

(n+1)^3=n^3+3(n)^2(1)+3(n)(1)^2+1^3

Somando e cancelando:

(n+1)^3=3(1^2+2^2+3^2+...+n^2)+3(1+2+3+...+n)+(n+1)

(n+1)^3-(n+1)=3Qn+3Sn

3Qn=(n+1)((n+1)^2-1)-3n(n+1)/2

3Qn=(n+1)(n^2+2n+1-1)-3n(n+1)/2

3Qn=(n+1)n(n+2)-3n(n+1)/2

3Qn=[2n(n+1)(n+2)-3n(n+1)]/2

Qn=n(n+1)[2(n+2)-3]/6=n(n+1)(2n+1)/6

Esta é a fórmula:

Qn=n(n+1)(2n+1)/6 ou Qn=n^3/3+n^2/2+n/6 (desenvolvendo)

Espero ter ajudado!

Olá! Vamos ajudar você nesta questão de soma dos termos de uma série.

Observe que todas os números envolvidos são número naturais.

Existe uma fórmula que permite soma dos quadrados dos n primeiros números naturais positivos, ou seja 1²+2²+...+n².

Esta fórmula é dada por:

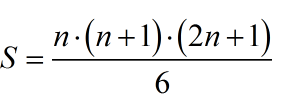
Aqui vai uma das possíveis demonstrações desta fórmula. Existem diversas demonstrações, umas não tão simples como as outras. Esta demontração advém do livro Matemáticas Gerais III, de Dias Agudo e Cândido da Silva.

De maneira geral, a soma S desejada pode ser representada pelo seguinte somatório:

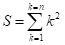
Considere agora a expansão da soma de cubos:

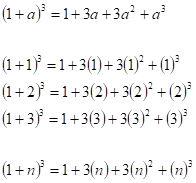
Repare que a expansão (1+1)³ é igual a 2³. O valor 2³ aparece no último membro da soma (1+2)³ por sua vez, e este comportamento se repete indefinidamente. Agora faremos a soma dos dois lados das igualdades, e iremos cancelando os valores (1+1)³ com o 2³ da linha subsequente, o termo (1+2)³ com o 3³ da linha subsequente, e assim sucessivamente. No final desta soma, tem-se:

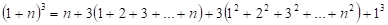
Agora, o termo 1+2+3+...+n é uma série conhecida:

Substituindo então e trabalhando esta igualdade, teremos:

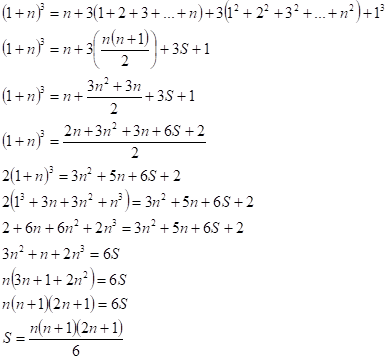
Assim está provado este somatório.