Qual o volume gerado quando a área entre o eixo x e o traçado de y = 2x^2 - x^3 gira em torno do eixo y=-2?

Estou resolvendo a apol = 05 o gabarito da está assim:

1=C  2=A 3=A 4=C 5=  6=C 7=A 8=B 9= 10=

FALTA A QUESTÃO 5,9 e 10 vou tentar resolver ate o final de semana se finalizar posto o gabarito

a quetsão 5, é a letra A se não me engano, 1296/5. Pelo menos foi o que achei nos cálculos.

Para calcular o volume, será utilizada a seguinte equação:

\(\Longrightarrow V = \int \limits_{a}^b \pi \Big [ f(x) -L \Big ] ^2 dx\)

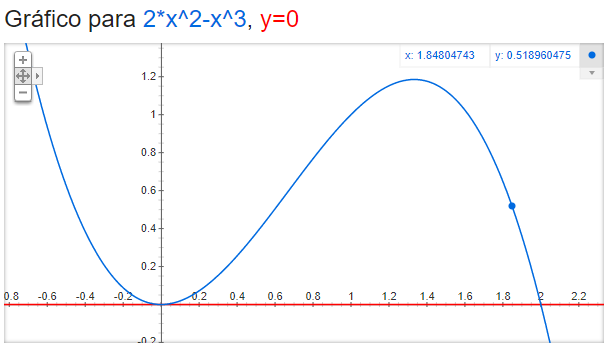
Os gráficos de \(f_1(x)=2x^2 - x^3\) e \(f_2(x)=0\) (eixo x) estão na figura a seguir:

Pelo gráfico, nota-se que a área é delimitada por \(a=0\) e \(b=2\). Como essa área gira em torno de \(L=-2\), tem-se que:

\(\Longrightarrow \int \limits_{a}^b \pi \Big [ f(x) -L \Big ] ^2 dx = \int \limits_{a}^b \pi \Big [ f_1(x) -L \Big ] ^2 dx - \int \limits_{a}^b \pi \Big [ f_2(x) -L \Big ] ^2 dx\)   \((I)\)

O valor do primeiro termo do lado direito da equação \((I)\) é:

\(\Longrightarrow \int \limits_{a}^b \pi \Big [ f_1(x) -L \Big ] ^2 dx = \int \limits_{0}^2 \pi \Big [ 2x^2 - x^3 -(-2) \Big ] ^2 dx\)

                                      \( = \int \limits_{0}^2 \pi \Big ( 2x^2 - x^3 +2 \Big ) ^2 dx\)

                                      \( = \int \limits_{0}^2 \pi ( 2x^2 - x^3 +2 )( 2x^2 - x^3 +2 ) dx\)

                                      \( = \pi \int \limits_{0}^2 ( x^6 - 4x^5 + 4x^4 - 4x^3 + 8x^2 + 4 ) dx\)

                                      \( = \pi \Big[ {1 \over 7}x^7 - {4 \over 6}x^6 + {4 \over 5}x^5 - {4 \over 4}x^4 + {8 \over 3}x^3 + 4x \Big ] \bigg | _{0}^2\)

\(\Longrightarrow \int \limits_{a}^b \pi \Big [ f_1(x) -L \Big ] ^2 dx = {1.528 \over 105}\pi\)     \((II)\)

O valor do segundo termo do lado direito da equação \((I)\) é:

\(\Longrightarrow \int \limits_{a}^b \pi \Big [ f_2(x) -L \Big ] ^2 dx = \int \limits_{0}^2 \pi \Big [ 0 -(-2) \Big ] ^2 dx\)

                                      \(= \int \limits_{0}^2 \pi \Big [ 2 \Big ] ^2 dx\)

                                      \(= 4 \pi\int \limits_{0}^2 dx\)

\(\Longrightarrow \int \limits_{a}^b \pi \Big [ f_2(x) -L \Big ] ^2 dx = 8 \pi\)     \((III)\)

Voltando à equação \((I)\), o volume é:

\(\Longrightarrow \int \limits_{a}^b \pi \Big [ f(x) -L \Big ] ^2 dx = \int \limits_{a}^b \pi \Big [ f_1(x) -L \Big ] ^2 dx - \int \limits_{a}^b \pi \Big [ f_2(x) -L \Big ] ^2 dx\)

\(\Longrightarrow V = {1.528 \over 105} \pi - 8\pi\)

\(\Longrightarrow \fbox {$ V = {688 \over 105} \pi $}\)