Dados A(2, 3) e B(3, 7), qual é a equação reduzida da reta r que passa por A e B?
💡 4 Respostas
Victor Bandeira
Determinar o coeficiente angular da reta.
m = (y2 – y1) / (x2 – x1)
m = (7-3)/(3-2)
m= 4/1
m=4
De acordo com o ponto A(2,3), temos:
y – y1 = m * (x – x1)
y-3=4*(x-2)
y-3=4x-8
y=4x-8+3
y=4x-5
RD Resoluções
Para responder à questão vamos usar conceitos de Geometria. A equação reduzida de uma reta é da forma onde
é o coeficiente angular e
é o coeficiente independente.
No nosso caso, olhando para os pontos e
, conseguimos a relação:
Da primeira equação conseguimos , que, substituindo na segunda equação:
Que nos dá
Portanto, a equação reduzida da reta é .
Andre Smaira
Para responder à questão vamos usar conceitos de Geometria. A equação reduzida de uma reta é da forma 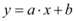 onde
onde  é o coeficiente angular e
é o coeficiente angular e  é o coeficiente independente.
é o coeficiente independente.
No nosso caso, olhando para os pontos  e
e  , conseguimos a relação:
, conseguimos a relação:
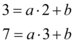
Da primeira equação conseguimos 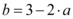 , que, substituindo na segunda equação:
, que, substituindo na segunda equação:
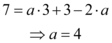
Que nos dá
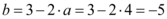
Portanto, a equação reduzida da reta é 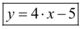 .
.
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta

Compartilhar