O que são "Separatrizes"?

Separatrizes são na Estatística também Medidas de Posição. As separatrizes - como o próprio nome sugere - são aquelas medidas que "separam" ou que dividem o conjunto em um certo número de partes iguais

Por exemplo, a mediana é uma separatriz, responsável por dividir uma sequência em \(2\) subsequências iguais entre si.

Outras separatrizes:

• Quartil (\(Q\)): é qualquer um dos \(3\) valores que divide o conjunto ordenado de dados em \(4\) partes iguais. Com isso, cada subsequência representa um quarto da amostra.
• Quintil (\(K\)): é qualquer um dos \(4\) valores que divide o conjunto ordenado de dados em \(5\) partes iguais. Com isso, cada subsequência representa um quinto da amostra.
• Decil (\(D\)): é qualquer um dos \(9\) valores que divide o conjunto ordenado de dados em \(10\) partes iguais. Com isso, cada subsequência representa um décimo da amostra.

Esse tipo de medida possui grande aplicação na área da Estatística.

Exemplo: estatura de alunos de uma escola.

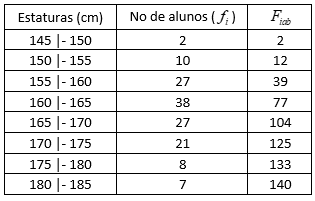
1561859870039

Onde \(f_i\) é a frequência absoluta simples da classe \(i\) e \(F_{iab}\) é a frequência acumulada.

1. Cálculo do primeiro quartil (\(Q_1\)): para determinar a posição do quartil \(E_{Q_1}\), utiliza-se a seguinte equação:


\[E_{Q_1}={i\cdot n \over 4}\]


Onde \(i\) é o número do quartil desejado e \(n\) é a quantidade de amostras.

Como se deseja o primeiro quartil, tem-se \(i=1\). Com um total de \(n=140\) amostras, o valor de \(E_{Q_1}\) é:


\[\begin{align} E_{Q_1} &={1 \cdot 140 \over 4} \\ &=35 \end{align}\]


Ou seja, \(Q_1\) está na posição \(35\). De acordo com a tabela, sua classe é \(155|-160\).

Para o cálculo de \(Q_1\), utiliza-se a seguinte equação:


\[Q_1=l+{h(E_{Q_1}-F_{ant}) \over f_{Q_1}}\]


Variáveis:

• \(l\): limite inferior da classe do quartil desejado.
• \(h\): amplitude do intervalo de classe. Fixo em \(h=5\text{ cm}\).
• \(E_{Q_1}\): elemento quartílico.
• \(F_{ant}\): frequência acumulada até a classe anterior à classe mediana,
• \(f_{Q_1}\): frequência absoluta simples da classe quartílica.

Portanto, o valor de \(Q_1\) é:


\[\begin{align} Q_1&=l+{h(E_{Q_1}-F_{ant}) \over f_{Q_1}} \\ &=155+{5(35-12) \over 27} \\ &=159,26 \end{align}\]


Ou seja, um quarto dos alunos possuem altura até \(159,26\text{ cm}\). Ou três quartos medem mais do que \(159,26\text{ cm}\).

1. Cálculo do nono decil (\(D_9\)): agora, tem-se \(i=9\). Portanto, o valor de \(E_{D_9}\) é:


\[\begin{align} E_{D_9}&={i\cdot n \over 10} \\ &={9\cdot 140 \over 10} \\ &= 126 \end{align}\]


Ou seja, \(D_9\) está na posição \(126\). De acordo com a tabela, sua classe é \(175|-180\). Analogamente ao que foi feito antes, o valor de \(D_9\) é:


\[\begin{align} D_9&=l+{h(E_{D_9}-F_{ant}) \over f_{D_9}} \\ &=175+{5(126-125) \over 8} \\ \\ &=175,63 \end{align}\]


Ou seja, \(90\%\) dos alunos possuem altura até \(175,63\text{ cm}\). Ou \(10\%\) medem mais do que \(175,63\text{ cm}\).

Resumidamente, as separatrizes são medidas que dividem sequências ordenadas em subsequências iguais entre si.