Indique a função que é solução da equação diferencial y" - 4y' + 4y = ex.
💡 3 Respostas
Andre Smaira
Contextualização:
Se y é uma função de x, e n é um inteiro positivo, então uma relação de igualdade (que não se reduz a uma identidade) que envolva x, y, y', y'', ...,y(n) é chamada uma equação diferencial de ordem n.
Equação diferencial é uma equação que apresenta derivadas ou diferenciais de uma função desconhecida (a incógnita da equação).
Classificação
Equação Diferencial Ordinária (EDO): Envolve derivadas de uma função de uma só variável independente.
Equação Diferencial Parcial (EDP): Envolve derivadas parciais de uma função de mais de uma variável independente.
Ordem: é a ordem da derivada de mais alta ordem da função incógnita que figura na equação.
Exemplos:

, tem ordem 1 e grau 1
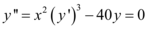
, tem ordem 2 e grau 3
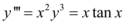
, tem ordem 3 e grau 3
Referência: https://www.somatematica.com.br/superior/equacoesdif/eq.php - Acessado em 12/10/2018
Resolução:
Primeiro calculando a solução homogênea teremos:
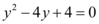
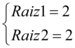
Repare que encontramos duas raízes iguais, logo na solução homogênea devemos multiplicar um dos termos por x:
Solução homogênea: 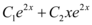
Agora devemos calcular a solução particular, usaremos o método dos coeficientes indeterminados.
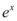
é uma constante A multiplicando 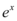 , logo teremos:
, logo teremos:
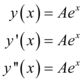
Note que todas as derivadas são iguais. Agora vamos substituir na equação principal:
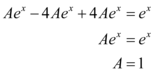
Como já era de se esperar, encontramos  , logo a solução da equação particular é
, logo a solução da equação particular é 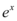 .
.
A solução geral é a soma da homogênea mais a particular, logo teremos como solução geral:
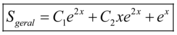
Conclusão:
Portanto, a solução geral da equação diferencial 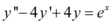 é:
é:
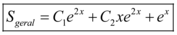
Andre Smaira
Contextualização:
Se y é uma função de x, e n é um inteiro positivo, então uma relação de igualdade (que não se reduz a uma identidade) que envolva x, y, y', y'', ...,y(n) é chamada uma equação diferencial de ordem n.
Equação diferencial é uma equação que apresenta derivadas ou diferenciais de uma função desconhecida (a incógnita da equação).
Classificação
Equação Diferencial Ordinária (EDO): Envolve derivadas de uma função de uma só variável independente.
Equação Diferencial Parcial (EDP): Envolve derivadas parciais de uma função de mais de uma variável independente.
Ordem: é a ordem da derivada de mais alta ordem da função incógnita que figura na equação.
Exemplos:
, tem ordem 1 e grau 1
, tem ordem 2 e grau 3
, tem ordem 3 e grau 3
Referência: https://www.somatematica.com.br/superior/equacoesdif/eq.php - Acessado em 12/10/2018
Resolução:
Primeiro calculando a solução homogênea teremos:
Repare que encontramos duas raízes iguais, logo na solução homogênea devemos multiplicar um dos termos por x:
Solução homogênea:
Agora devemos calcular a solução particular, usaremos o método dos coeficientes indeterminados.
é uma constante A multiplicando , logo teremos:
Note que todas as derivadas são iguais. Agora vamos substituir na equação principal:
Como já era de se esperar, encontramos , logo a solução da equação particular é
.
A solução geral é a soma da homogênea mais a particular, logo teremos como solução geral:
Conclusão:
Portanto, a solução geral da equação diferencial é:
RD Resoluções
Contextualização:
Se y é uma função de x, e n é um inteiro positivo, então uma relação de igualdade (que não se reduz a uma identidade) que envolva x, y, y', y'', ...,y(n) é chamada uma equação diferencial de ordem n.
Equação diferencial é uma equação que apresenta derivadas ou diferenciais de uma função desconhecida (a incógnita da equação).
Classificação
Equação Diferencial Ordinária (EDO): Envolve derivadas de uma função de uma só variável independente.
Equação Diferencial Parcial (EDP): Envolve derivadas parciais de uma função de mais de uma variável independente.
Ordem: é a ordem da derivada de mais alta ordem da função incógnita que figura na equação.
Exemplos:
, tem ordem 1 e grau 1
, tem ordem 2 e grau 3
, tem ordem 3 e grau 3
Referência: https://www.somatematica.com.br/superior/equacoesdif/eq.php - Acessado em 12/10/2018
Resolução:
Primeiro calculando a solução homogênea teremos:
Repare que encontramos duas raízes iguais, logo na solução homogênea devemos multiplicar um dos termos por x:
Solução homogênea:
Agora devemos calcular a solução particular, usaremos o método dos coeficientes indeterminados.
é uma constante A multiplicando , logo teremos:
Note que todas as derivadas são iguais. Agora vamos substituir na equação principal:
Como já era de se esperar, encontramos , logo a solução da equação particular é
.
A solução geral é a soma da homogênea mais a particular, logo teremos como solução geral:
Conclusão:
Portanto, a solução geral da equação diferencial é:
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta




Compartilhar