o campo magnético resultante em uma região do espaço depende da posição x e é dado por:
Β= µ.i_x Κ. para 0 < x ≤ 4.00cm.
2π(x²+a²)²
Se a= 4,00cm e i é a corrente que circula no fio condutor que gera o campo, determine o(s) valor(s) de x para os quais o módulo do campo magnético é máximo.
Dica: Lembre-se que a derivada de uma função é nula no valor máximo/mínimo da função.
💡 2 Respostas
RD Resoluções
Para resolver este problema, devemos colocar em prática nosso conhecimento sobre campo magnético e derivada de uma função.
_________________________________________________________________________
O campo elétrico dado é 
. Substituindo o valor de “a” na expressão:
Para calcular o valor de x para o qual o módulo do campo magnético é máximo, devemos derivar a expressão em x, pois a derivada se anula no valor máximo ou mínimo da função.
O termo
não pode ser nulo, pois é constante diferente de zero. O termo 
também é diferente de zero, pois é um termo quadrático.
Dessa forma, 
Basta resolver a equação acima.
_________________________________________________________________________
Como o enunciado impõe que 
, temos que 
Andre Smaira
Para resolver este problema, devemos colocar em prática nosso conhecimento sobre campo magnético e derivada de uma função.
_________________________________________________________________________
O campo elétrico dado é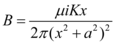 
. Substituindo o valor de “a” na expressão:
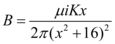
Para calcular o valor de x para o qual o módulo do campo magnético é máximo, devemos derivar a expressão em x, pois a derivada se anula no valor máximo ou mínimo da função.
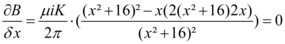
O termo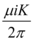
não pode ser nulo, pois é constante diferente de zero. O termo 
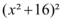também é diferente de zero, pois é um termo quadrático.
Dessa forma,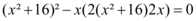 
Basta resolver a equação acima.
_________________________________________________________________________
Como o enunciado impõe que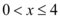 
, temos que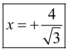 
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Outros materiais
Perguntas relacionadas
O motor de indução trifásico tem seu princípio de funcionamento baseado no campo magnético girante, que é o campo magnético resultante da interação...
Máquinas Elétricas e Transformadores
•UNINORTE
edmar
Materiais relacionados
Compartilhar