Respostas
RD Resoluções
Contextualização:
Definição: Um vetor (geométrico) no espaço R³ é uma classe de objetos matemáticos (segmentos de reta) que tem a mesma direção, mesmo sentido e mesma intensidade. Esta classe de equivalência de objetos com as mesmas características é representada por um segmento de reta desta família (representante).
O representante escolhido, quase sempre é o vetor v cuja origem é (0,0,0) e extremidade é o terno ordenado (a,b,c) do espaço R³, razão pela qual denotamos este vetor por: v=(a,b,c).
Se a origem do vetor não é a origem (0,0,0) do sistema R³, realizamos a diferença entre a extremidade e a origem do vetor. Por exemplo, se um vetor v tem origem em (1,2,3) e extremidade em (7,12,15), ele é dado por v=(6,10,12), pois:
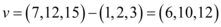
Produto de vetor por escalar:
Se v=(a, b, c) e k é um número real, definimos a multiplicação de k por v, como:
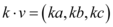
Módulo de um vetor e vetores unitários:
O módulo ou comprimento do vetor v=(x,y,z) é definido por:
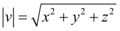
Resolução:
Dado o vetor 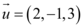 , iremos julgar as assertivas abaixo:
, iremos julgar as assertivas abaixo:
I – o vetor 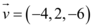 possui sentido contrário de
possui sentido contrário de  e
e 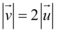 ;
;
Se tomarmos como base que o vetor  foi multiplicado por uma constante escalar de valor (-2), podemos concluir que:
foi multiplicado por uma constante escalar de valor (-2), podemos concluir que:
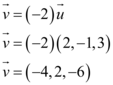
Sendo assim, o vetor  possui sentido contrário de
possui sentido contrário de  . E no cálculo dos módulos, temos:
. E no cálculo dos módulos, temos:
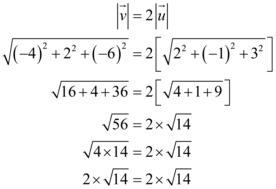
Portanto, assertiva I está correta.
II – o vetor 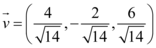 possui o mesmo sentido de
possui o mesmo sentido de  e
e  .
.
Se tomarmos como base que o vetor  foi multiplicado por uma constante escalar de valor
foi multiplicado por uma constante escalar de valor 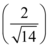 , podemos concluir que:
, podemos concluir que:
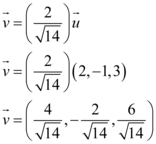
Sendo assim, o vetor  possui o mesmo sentido de
possui o mesmo sentido de  .
.
E o cálculo de  é:
é:
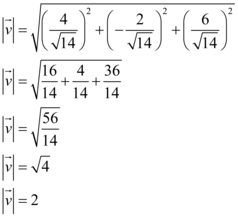
Portanto, assertiva II também está correta.
III – o vetor 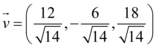 possui o mesmo sentido de
possui o mesmo sentido de  e
e  .
.
Se tomarmos como base que o vetor  foi multiplicado por uma constante escalar de valor
foi multiplicado por uma constante escalar de valor 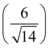 , podemos concluir que o vetor
, podemos concluir que o vetor  possui o mesmo sentido de
possui o mesmo sentido de  .
.
E o cálculo de  é:
é:
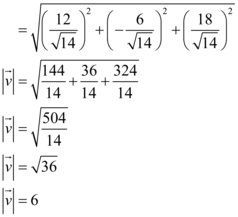
Portanto, assertiva III também está correta.
IV – o vetor 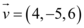 é paralelo ao vetor
é paralelo ao vetor 
Para que o vetor  seja paralelo ao vetor
seja paralelo ao vetor  , o vetor
, o vetor  precisa ser multiplicado por uma constante.
precisa ser multiplicado por uma constante.
Como o vetor 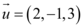 , podemos observar que o vetor
, podemos observar que o vetor 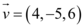 não é multiplicado por uma mesma constante.
não é multiplicado por uma mesma constante.
Portanto, a assertiva IV está incorreta.
Sendo assim, a alternativa correta é a alternativa b., que afirma que apenas as assertivas I, II e III estão corretas.
Conclusão:
Conforme mostrado acima, as assertivas I, II e III estão corretas, enquanto a assertiva IV está incorreta.
Portanto, a alternativa correta é a alternativa b.
Responda
Para escrever sua resposta aqui, entre ou crie uma conta


