per de eletromagnetismo

qualquer dúvida só falar.

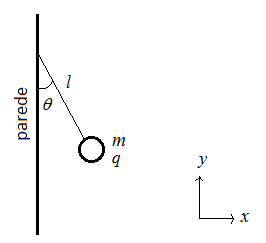
Autoria Própria

---

A parede carregada irá gerar um campo elétrico na direção do eixo \(x\). Logo, a partícula de massa \(m\) sofrerá a influencia de uma força \({\vec F}\) na mesma direção, que é a responsável pelo ângulo \(\theta\). Sendo \(\left| {\vec F} \right|\) o módulo da força \({\vec F}\), podemos determinar sua intensidade por meio do triângulo retângulo formado com o fio, a parede e a força. Assim, podemos fazer com \(l = 0,1{\text{ m}}\):

\[\eqalign{ \left| {\vec F} \right| = l \cdot \sin \theta \cr = 0,1 \cdot \sin \left( {2,3^\circ } \right) \cr \cong 4 \cdot {10^{ - 3}}{\text{ N}} }\]

---

Como a intensidade do campo elétrico \({\vec E}\) é dada por \(\left| {\vec E} \right| = \dfrac{{\left| {\vec F} \right|}}{q}\), onde \(q\) é a carga elétrica, temos do enunciado:

\[\eqalign{ \left| {\vec E} \right| &= \dfrac{{\left| {\vec F} \right|}}{q}\cr&= \dfrac{{4 \cdot {{10}^{ - 3}}{\text{ N}}}}{{1,7 \cdot {{10}^{ - 9}}{\text{ C}}}}\cr&= 2,35 \cdot {10^6}{\text{ N/C}} }\]

---

Portanto, temos que \(\boxed{\left| {\vec E} \right| = 2,35 \cdot {{10}^6}{\text{ N/C}}}\).