Uma linha infinita de cargas produz um campo de módulo 4,5 × 104 N/C a uma distância de 2,0 m. Calcule a densidade linear de cargas??

.......

\
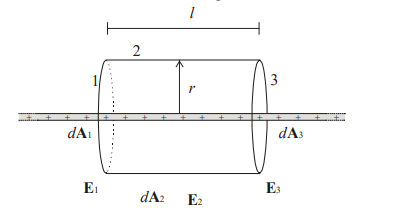
Situação retratada.

Aplicando a Lei de Gauss, obtemos:

\[\oint E * d_A = \dfrac{\sum q}{\epsilon_0}\]

\[\int_1 E * d_A + \int_2 E * d_A + \int_3 E * d_A = \dfrac{\lambda l}{\epsilon_0}\]

Neste caso, as integrais 1 e 3 podem ser consideradas nulas, já que o ângulo entre os vetores \(E\)e \(d_A\)é \(90^{\circ}\) Assim:

\[0 + \int_2 E * d_A * \cos 0 + 0 = \dfrac{\lambda l}{\epsilon_0}\]

\[E \int_2 d_A = \dfrac{\lambda l}{\epsilon_0}\lambda = 2 \pi * (8,85 * 10^{-12} Nm^2/C^2)(2,0 m)(4,0 * 10^{4}N/C) = 4,44849 * 10^{-6} C/m\]

Assim, tem-se:

\[\boxed{\lambda \approx 4,45 \mu C/m}\]