estou co dúvidas na questão abaixo

É importante salientar que nas transformações lineares não é necessário provar que os espaços trabalhados são vetoriais, pois presumimos que eles são espaços vetoriais.

Texto elaborado pelo Professor, 2019.

Levando em consideração esses fatos, julgue as proposições abaixo:

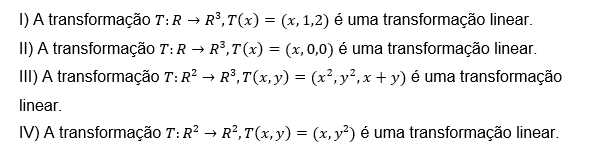
Estão corretas:

Geometria Analítica

•

UNICESUMAR

6

0

6

0

6

Fernando Jesus Monteiro

16/09/2019

💡 6 Respostas

Bianca Lima

17.09.2019

cade as alternativas?

0

Andre Smaira

12.10.2019

Dada uma transformação

T:V \to W

sendo

\(V\)

e

\(W\)

espaços vetoriais, ela será linear se satisfazer a condição

T\left( {\alpha \cdot {v_1} + \beta \cdot {v_2}} \right) = \alpha \cdot T\left( {{v_1}} \right) + \beta \cdot T\left( {{v_2}} \right)

onde

{v_1}

e

{v_2}

são vetores de

\(V\)

Para a transformação linear da primeira proposição, sejam ${v_1} = {x_1}$ e ${v_2} = {x_2}$ Substituindo na condição, temos:

$\eqalign{ T\left( {\alpha \cdot {x_1} + \beta \cdot {x_2}} \right) = \left( {\alpha \cdot {x_1} + \beta \cdot {x_2},1,2} \right) \cr = \left( {\alpha \cdot {x_1},1,2} \right) + \left( {\beta \cdot {x_2},0,0} \right) \cr \ne \alpha \cdot T\left( {{v_1}} \right) + \beta \cdot T\left( {{v_2}} \right) }$

Assim, a primeira transformação não é linear. Analogamente, para a transformação da segunda proposição com ${v_1} = {x_1}$ e ${v_2} = {x_2}$ :

$\eqalign{ T\left( {\alpha \cdot {x_1} + \beta \cdot {x_2}} \right) &= \left( {\alpha \cdot {x_1} + \beta \cdot {x_2},0,0} \right)\cr &= \left( {\alpha \cdot {x_1},0,0} \right) + \left( {\beta \cdot {x_2},0,0} \right)\cr &= \alpha \cdot \left( {{x_1},0,0} \right) + \beta \cdot \left( {{x_2},0,0} \right)\cr &= \alpha \cdot T\left( {{v_1}} \right) + \beta \cdot T\left( {{v_2}} \right) }$

Assim, a segunda transformação é linear. Para a transformação da terceira proposição, sejam ${v_1} = \left( {{x_1},{y_1}} \right)$ e ${v_2} = \left( {{x_2},{y_2}} \right)$ Substituindo na condição, temos:

$\eqalign{ T\left( {\alpha \cdot \left( {{x_1},{y_1}} \right) + \beta \cdot \left( {{x_2},{y_2}} \right)} \right) = T\left( {\left( {\alpha {x_1},\alpha {y_1}} \right) + \left( {\beta {x_2},\beta {y_2}} \right)} \right) \cr = T\left( {\alpha {x_1} + \beta {x_2},\alpha {y_1} + \beta {y_2}} \right) \cr = \left( {{{\left( {\alpha {x_1} + \beta {x_2}} \right)}^2},{{\left( {\alpha {y_1} + \beta {y_2}} \right)}^2},\alpha {x_1} + \beta {x_2} + \alpha {y_1} + \beta {y_2}} \right) \cr = \left( {{\alpha ^2}{x_1}^2 + {\beta ^2}{x_2}^2 + 2\alpha \beta {x_1}{x_2},{\alpha ^2}{y_1}^2 + {\beta ^2}{y_2}^2 + 2\alpha \beta {y_1}{y_2},\alpha \left( {{x_1} + {y_1}} \right) + \beta \left( {{x_2} + {y_2}} \right)} \right) \cr \ne \alpha \cdot T\left( {{v_1}} \right) + \beta \cdot T\left( {{v_2}} \right) }$

Assim, a terceira transformação não é linear. E, para a transformação da quarta proposição, considerando ${v_1} = \left( {{x_1},{y_1}} \right)$ e ${v_2} = \left( {{x_2},{y_2}} \right)$ temos:

$\eqalign{ T\left( {\alpha \cdot \left( {{x_1},{y_1}} \right) + \beta \cdot \left( {{x_2},{y_2}} \right)} \right) = T\left( {\left( {\alpha {x_1},\alpha {y_1}} \right) + \left( {\beta {x_2},\beta {y_2}} \right)} \right) \cr = T\left( {\alpha {x_1} + \beta {x_2},\alpha {y_1} + \beta {y_2}} \right) \cr = \left( {\alpha {x_1} + \beta {x_2},{{\left( {\alpha {y_1} + \beta {y_2}} \right)}^2}} \right) \cr = \left( {\alpha {x_1} + \beta {x_2},{\alpha ^2}{y_1}^2 + {\beta ^2}{y_2}^2 + 2\alpha \beta {y_1}{y_2}} \right) \cr = \left( {\alpha {x_1},{\alpha ^2}{y_1}^2} \right) + \left( {\beta {x_2},{\beta ^2}{y_2}^2 + 2\alpha \beta {y_1}{y_2}} \right) \cr \ne \alpha \cdot T\left( {{v_1}} \right) + \beta \cdot T\left( {{v_2}} \right) }$

Assim, a quarta transformação não é linear.

Portanto, a proposição II) é a correta.

0