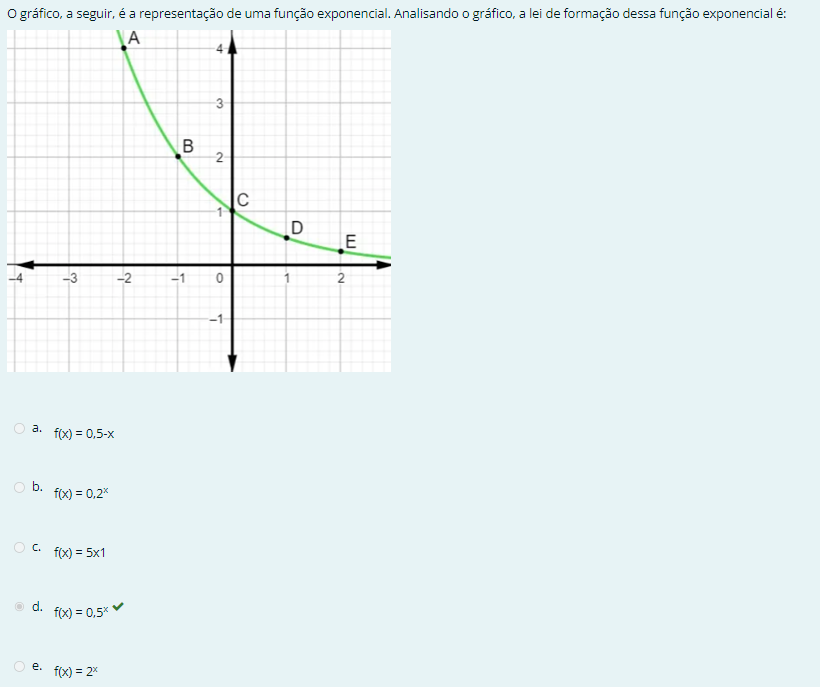
Para determinar a lei de formação da função exponencial a partir do gráfico, precisamos considerar as características típicas de funções exponenciais, que geralmente têm a forma \( f(x) = a \cdot b^x \), onde \( a \) é uma constante e \( b \) é a base da exponencial. Vamos analisar as alternativas: a. \( f(x) = 0,5^{-x} \) - Esta é uma função exponencial decrescente, pois a base é menor que 1 e o expoente é negativo. b. \( f(x) = 0,2 \) - Esta é uma função constante, não uma exponencial. c. \( f(x) = 5x^1 \) - Esta é uma função linear, não exponencial. d. \( f(x) = 0,5 \) - Esta também é uma função constante, não exponencial. e. \( f(x) = 2^x \) - Esta é uma função exponencial crescente, pois a base é maior que 1. Sem o gráfico para visualizar, a opção que mais se aproxima de uma função exponencial é a) \( f(x) = 0,5^{-x} \), pois representa uma função exponencial decrescente. Portanto, a resposta correta é a) \( f(x) = 0,5^{-x} \).