Como é o gráfico de euler e Ln?

Para responder tal pergunta, devemos colocar em prática nosso conhecimento sobre funções.

A função exponencial trata-se da \(y=f(x)=e^x\). Seu gráfico está exibido abaixo.

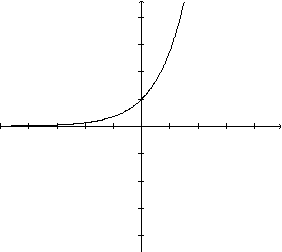
Fonte: http://ecalculo.if.usp.br/funcoes/exponencial/fexponencial.htm (Acesso 23 mai. 2018).

No gráfico, cada ponto possui a forma \((x,\text{ } e^x)\), uma vez que a ordenada é o resultado de \(e^x\), isto é , a exponencial na base do número de euler de \(x\).

O dominío da função \(y=e^x\)  é o conjunto \(R=]- \infty, \infty[\) e a imagem é o conjunto \(R_+^*=]0,+\infty[.\)

No gráfico, o eixo horizontal é uma assíntota.

Por sua vez, a função logarítmica natural trata-se da \(y=f(x)=\ln(x)\). Seu gráfico está exibido abaixo.

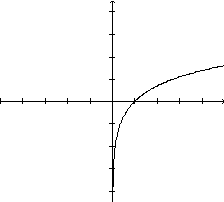
Fonte: http://ecalculo.if.usp.br/funcoes/logaritmica/flogaritmica.htm (Acesso 23 mai. 2018).

No gráfico, cada ponto possui a forma \((x,\text{ } \ln x)\), uma vez que a ordenada é o resultado de \(\ln x\), isto é , o logarítimo natural do número \(x\).

O dominío da função \(y=\ln x\)  é o conjunto \(R_+^* =]0, \infty[\) e a imagem é o conjunto \(R=]- \infty,+\infty[.\)

No gráfico, o eixo vertical é uma assíntota.