alguém tem a demonstração do teorema de papus sem usar cálculo diferencial

Teorema 1

Se um arco C de uma curva suave localizada em um plano, for girado em um ângulo θ(0≤θ≤2π) em torno de um eixo localizado em um plano, e que não intercepta o arco C, a área da superfície gerada pelo arco Cà medida que ele gira o ângulo θ é igual ao comprimento de C vezes o comprimento da trajetória percorrida pelo centróide de C durante a rotação θ.

Se o comprimento do arco é Le ρé a distância do eixo de rotação ao centróide do arco, a área da superfície Sgerada pelo arco à medida que ele gira em um ângulo θ é:

S = Lρθ

Demonstração:

dS = θyds → S = = θ 

=  → L = ds = S = Lθ para 0≤θ≤2π, c.q.d.

EXEMPLO:

Deduzir a fórmula para área S da superfície externa do cone reto circular sólido.

TEOREMA 2

Se uma área Alocalizada em um plano for girada em um ângulo θ (0≤θ≤2π)em torno de um eixo localizado em um plano que não intercepta a área A, o volume gerado pela área A, à medida em que ele gira o ângulo θ, é igual à área Avezes o comprimento da trajetória percorrida pelo centróide de Adurante a rotação θ.

Se ρé a distância do eixo de rotação ao centróide da área plana, o volume V gerado pela área, à medida em que ele gira em um ângulo θ é:

V=Aρθ

Demonstração:

EXEMPLO:

Deduzir a fórmula para o volume V do cone reto circular sólido.

O Teorema de Pappus-Guldinus nos fornece métodos para cálculo de volume e área superficial de objetos de revolução. 

Considere a função abaixo:

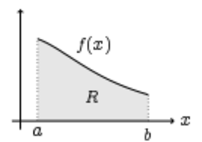
Para cálculo do volume   de um sólido formado pela revolução de uma função   no intervalo  ,  usamos:

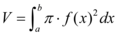
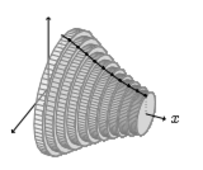
Repare que a equação fornecida usa do princípio de somar áreas de círculos infinitesimais de raio   pelo intervalo, ora, a área do círculo é dada por 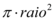 , justificando a função de integração. Geometricamente estamos calculando o volume da figura:

E, para a área superficial    dessa mesma função no intervalo:

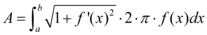
Da mesma forma, usamos a equação do perímetro de um círculo de raio  , ou seja, 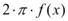 , multiplicado do comprimento do arco.

Fonte:

https://e-scola.edu.gov.cv/index.php?option=com_rea&id_disciplina=1&id_materia=6&id_capitulo=72&Itemid=220 

Para entendermos o Teorema de Pappus-Guldinus precisamos de conceitos de Cálculo e noções de geometria. Vamos tentar demonstrar geometricamente o Teorema.

O Teorema de Pappus-Guldinus nos fornece métodos para cálculo de volume e área superficial de objetos de revolução.

Considere a função abaixo:

Para cálculo do volume de um sólido formado pela revolução de uma função no intervalo , usamos:

Repare que a equação fornecida usa do princípio de somar áreas de círculos infinitesimais de raio pelo intervalo, ora, a área do círculo é dada por , justificando a função de integração. Geometricamente estamos calculando o volume da figura:

E, para a área superficial dessa mesma função no intervalo:

Da mesma forma, usamos a equação do perímetro de um círculo de raio , ou seja, , multiplicado do comprimento do arco.

Fonte:

https://e-scola.edu.gov.cv/index.php?option=com_rea&id_disciplina=1&id_materia=6&id_capitulo=72&Itemid=220