Respostas
Andre Smaira
Foi usado conhecimento sobre álgebra linear para resolução dessa questão.
Usaremos o Teorema do Núcleo – Imagem para resolução dessa questão, nele diz que “Seja 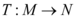 uma transformação linear de M para N, se
uma transformação linear de M para N, se 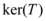 é o núcleo dessa transformação e
é o núcleo dessa transformação e 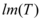 a imagem da transformação, temos então que
a imagem da transformação, temos então que 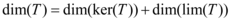 onde
onde  , denota a dimensão do espaço gerado por T,
, denota a dimensão do espaço gerado por T, 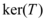 ,
, 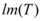 .”
.”
a)
Suponha que exista 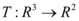 injetora, como T é injetora temos que
injetora, como T é injetora temos que 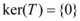 , deste modo então:
, deste modo então:
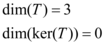
Assim pelo teorema temos:
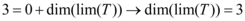
Porém como 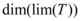 é no máximo igual a 2 pois
é no máximo igual a 2 pois 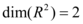 essa transformação não pode existir.
essa transformação não pode existir.
b)
Vamos fazer como fizemos anteriormente, suponhamos que 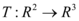 seja sobrejetora, como T é sobrejetora temos que
seja sobrejetora, como T é sobrejetora temos que 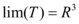 o que nos leva a:
o que nos leva a:
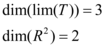
Com o teorema temos que:
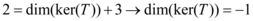
Como a dimensão de um espaço não pode ser um valor negativo não é possível a transformação.
Ambas transformações não são verdadeiras.
Andre Smaira
Foi usado conhecimento sobre álgebra linear para resolução dessa questão.
Usaremos o Teorema do Núcleo – Imagem para resolução dessa questão, nele diz que “Seja uma transformação linear de M para N, se
é o núcleo dessa transformação e
a imagem da transformação, temos então que
onde
, denota a dimensão do espaço gerado por T,
,
.”
a)
Suponha que exista injetora, como T é injetora temos que
, deste modo então:
Assim pelo teorema temos:
Porém como é no máximo igual a 2 pois
essa transformação não pode existir.
b)
Vamos fazer como fizemos anteriormente, suponhamos que seja sobrejetora, como T é sobrejetora temos que
o que nos leva a:
Com o teorema temos que:
Como a dimensão de um espaço não pode ser um valor negativo não é possível a transformação.
Ambas transformações não são verdadeiras.
RD Resoluções
Foi usado conhecimento sobre álgebra linear para resolução dessa questão.
Usaremos o Teorema do Núcleo – Imagem para resolução dessa questão, nele diz que “Seja uma transformação linear de M para N, se
é o núcleo dessa transformação e
a imagem da transformação, temos então que
onde
, denota a dimensão do espaço gerado por T,
,
.”
a)
Suponha que exista injetora, como T é injetora temos que
, deste modo então:
Assim pelo teorema temos:
Porém como é no máximo igual a 2 pois
essa transformação não pode existir.
b)
Vamos fazer como fizemos anteriormente, suponhamos que seja sobrejetora, como T é sobrejetora temos que
o que nos leva a:
Com o teorema temos que:
Como a dimensão de um espaço não pode ser um valor negativo não é possível a transformação.
Ambas transformações não são verdadeiras.
Responda
Para escrever sua resposta aqui, entre ou crie uma conta




