Preciso de ajuda para a resolução dessa questão. Obrigada !
💡 5 Respostas
Giovani Ferreira Jr.
c ésta correta
Rihan Cavalcante Chalegre
a) Os pontos em que a bola toca no solo, são os pontos onde a função h(d) que representa a trajetória da bola são iguais a 0, conhecidos também como as raízes da função, então:
h(d) = 0
-0,398d² + 5,572d = 0
d(-0,398d + 5,572) = 0
d' = 0 metros e d'' = 5,572/0,398 = 14 metros
Portanto, a distância horizontal percorrida pela bola é de 14 metros.
b) Para encontrar a altura máxima dessa função devemos observar onde a inclinação da reta tangente a função é igual a 0. Como a derivada representa a inclinação da reta tangente a função, basta apenas derivar e igualar a 0 a derivada, porque no ponto máximo da parábola, a inclinação da reta tangente a função é igual a 0.
h'(d) = 0
-0,796d + 5,572 = 0
d = 5,572/0,796
d = 7 metros
Aplicando na função, encontraremos a altura máxima atingida pela bola:
h(7) = -0,398(7)² + 5,572(7)
h(7) = 19,502 metros
Portanto, a altura máxima atingida pela bola foi 19,502 metros.
c) 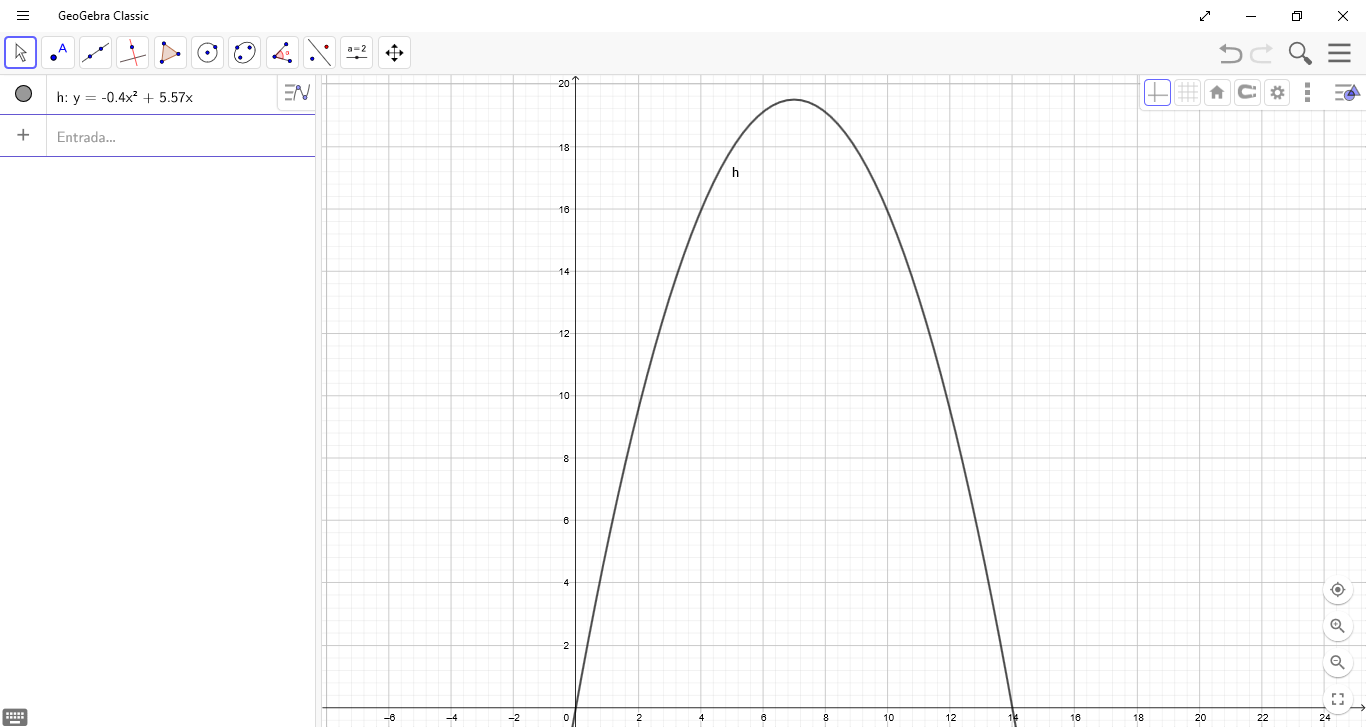
Andre Smaira
Nesse exercício vamos analisar o movimento da bola.
a) A bola toca o chão quando sua altura é nula:
$$h(d)=0=-0,398d^2+5,572d =(-0,398d+5,572)d \Rightarrow \boxed{d=14\ m}$$
b) A altura máxima ocorre no vértice da parábola:
$$h_m=-{\Delta\over4a}=-{5,572^2\over-4\cdot0,398}\Rightarrow \boxed{h_m=19,5\ m}$$
c) Vamos agora desenhar o gráfico da função usando o site google.com:
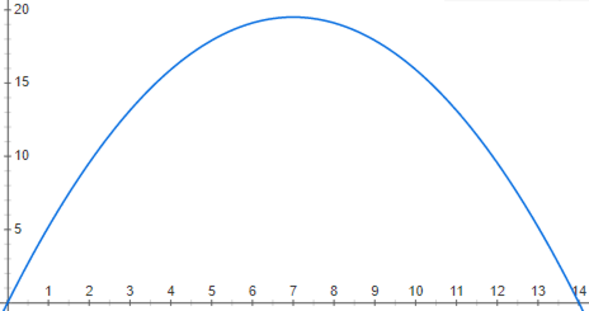
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Materiais relacionados
 3 pág.
3 pág.




Compartilhar