MHS - PÊNDULO SIMPLES E AMORTECIDO

Kjj

---

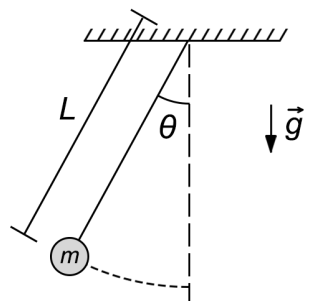
Para este caso, as únicas forças que atuam na partícula de massa \(m\) são a força peso e a força de tração do fio de comprimento \(L\), considerado inextensível. A posição será denotada pelo angulo \(\theta\). Por meio das forças que atuam na partícula, podemos encontrar as seguintes fórmulas para a posição \(\theta \left( t \right)\), a velocidade angular \(\omega \left( t \right)\), a aceleração \(\alpha \left( t \right)\), o período \(T\), a energia cinética \(K\) e a energia potencial \(U\):

\[\left\{ \matrix{ \theta \left( t \right) = A\cos \left( {\omega t + {\theta _0}} \right) \cr \omega \left( t \right) = {{d\theta } \over {dt}} \cr \alpha \left( t \right) = {{{d^2}\theta } \over {d{t^2}}} \cr T = 2\pi \sqrt {{L \over g}} \cr K\left( t \right) = {{mv{{\left( t \right)}^2}} \over 2} \cr U\left( t \right) = mgh\left( t \right) } \right.\]

\[\eqalign{ A:{\text{ amplitude}} \cr {\theta _0}:{\text{ posição angular inicial}} \cr v\left( t \right):{\text{ velocidade no instante }}t \cr h\left( t \right):{\text{ altura da partícula}} }\]

---

Quando a partícula sofre a influência de uma força resistiva \(F = - b\vec v\), temos o caso do pêndulo amortecido. Para esse caso, as equações são:

\[\left\{ \matrix{ \theta \left( t \right) = A{e^{ - {b \over {2m}}t}}\cos \left( {\omega t + {\theta _0}} \right) \cr \omega \left( t \right) = {{d\theta } \over {dt}} \cr \alpha \left( t \right) = {{{d^2}\theta } \over {d{t^2}}} \cr T = 2\pi \sqrt {{L \over g}} \cr K\left( t \right) = {{mv{{\left( t \right)}^2}} \over 2} \cr U\left( t \right) = mgh\left( t \right) } \right.\]

---

Portanto, para o pêndulo simples e o amortecido, a equação da posição é \(\boxed{\theta \left( t \right) = A\cos \left( {\omega t + {\theta _0}} \right)}\) e \(\boxed{\theta \left( t \right) = A{e^{ - \dfrac{b}{{2m}}t}}\cos \left( {\omega t + {\theta _0}} \right)}\), respectivamente. Para a velocidade e aceleração angular, período, energia cinética e potencial, temos \(\boxed{\omega \left( t \right) = \dfrac{{d\theta }}{{dt}}}\), \(\boxed{\alpha \left( t \right) = \dfrac{{{d^2}\theta }}{{d{t^2}}}}\), \(\boxed{T = 2\pi \sqrt {\dfrac{L}{g}} }\), \(\boxed{K\left( t \right) = \dfrac{{mv{{\left( t \right)}^2}}}{2}}\) e \(\boxed{U\left( t \right) = mgh\left( t \right)}\).