Exercícios de Equação de Bernoulli, Tensão de Cisalhamento, Medidores de Vazão (Pitot, venturi) resolvidos? Obrigada
💡 1 Resposta
Ton Silva
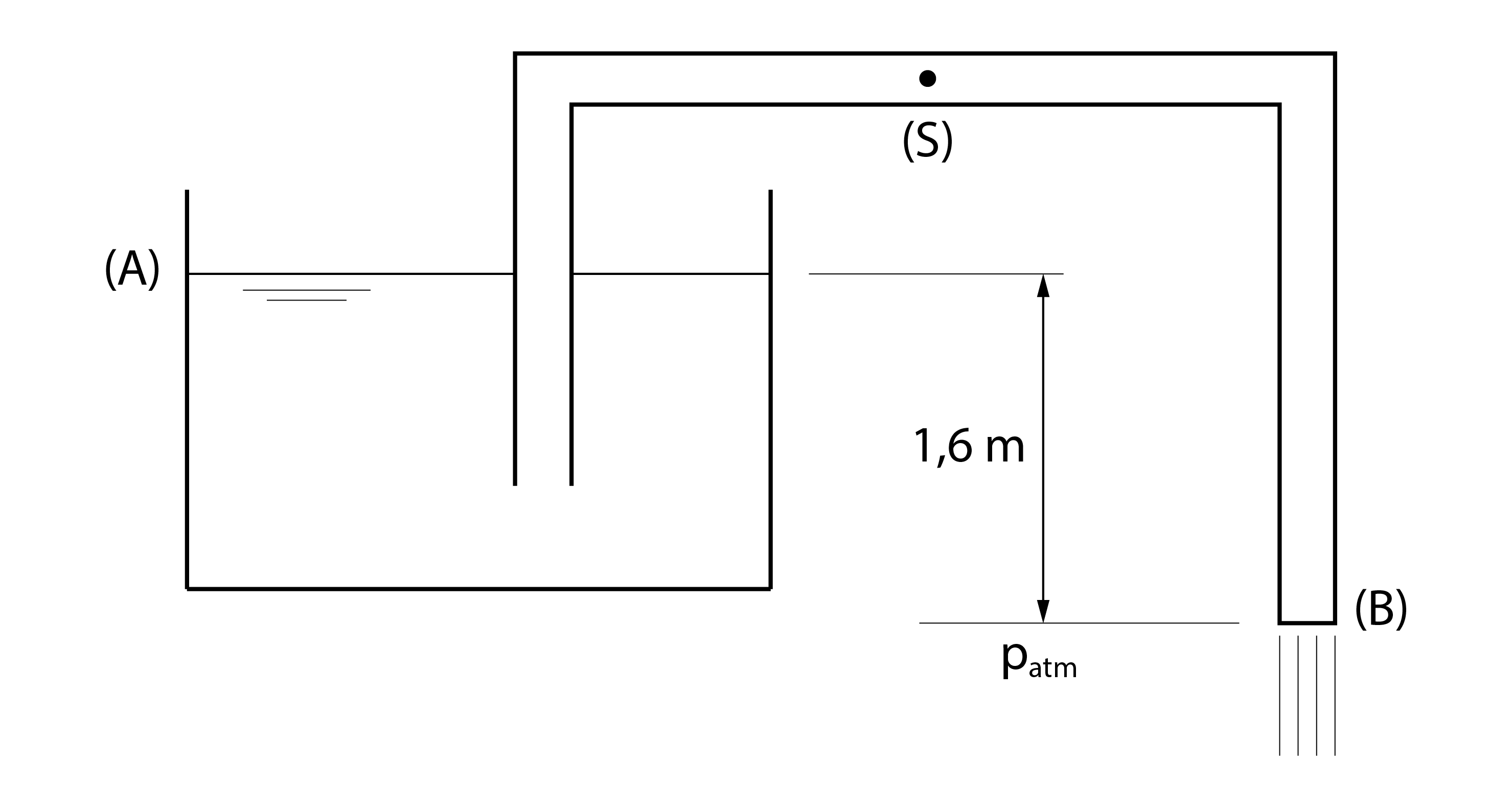
A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto S do sifão deve ser maior que – 60 kPa em pressão relativa e desprezando as perdas de carga determine a velocidade do fluido no sifão e a máxima altura que o ponto S pode ter em relação ao ponto A.
ESQUEMA DO EXERCÍCIO 1
Resolução
Para a resolução da questão, vamos inicialmente determinar a velocidade de fluxo no sifão.
Sabendo que a velocidade de escoamento em todo o sifão é a mesma, podemos utilizar a equação de Bernoulli entre os pontos A e B para determinar tal velocidade. Temos então que:
\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma }}
zA
+2⋅g
vA
2
+γ
pA
=zB
+2⋅g
vB
2
+γ
pB
Como temos que a pressão em ambos os pontos é a própria pressão atmosférica e que a velocidade no ponto A é nula, temos:
\mathrm{{z_A} = \dfrac{{v_B^2}}{{2 \cdot g}}}
zA
=2⋅g
vB
2
\mathbf{{v_B} = 5,66m/s}
vB
=5,66m/s
Agora que já temos o valor da velocidade do fluxo no sifão, podemos aplicar a equação de Bernoulli entre os pontos A e S.
Como temos que a pressão mínima no ponto S é -60 kPa e considerando agora o plano horizontal de referência passando pelo ponto A, temos:
\mathrm{0 = {z_S} + \dfrac{{5,{{66}^2}}}{{2 \cdot g}} - \dfrac{{60 \cdot {{10}^3}}}{{{{10}^4}}}}
0=zS
+2⋅g
5,662
−104
60⋅103
\mathbf{{z_S} = 4,4m}
zS
=4,4m
Exercício 2
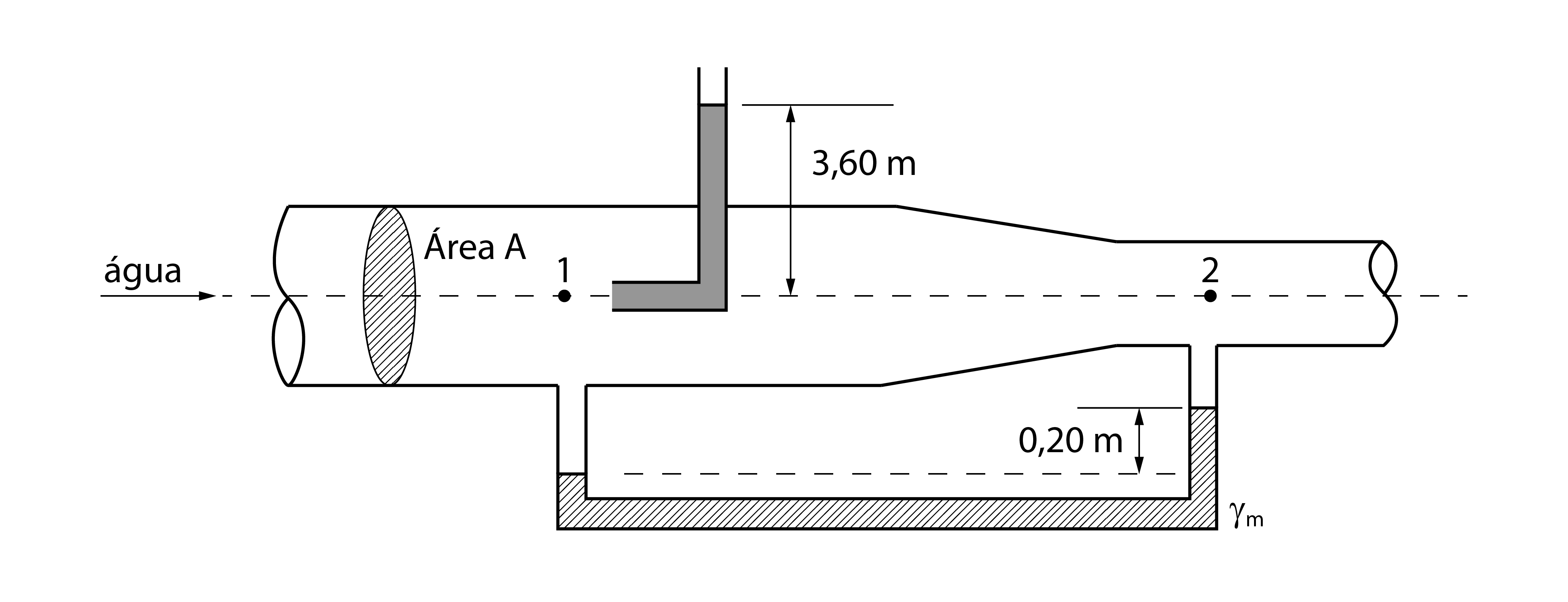
Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:
- \mathrm{\gamma _a}
- γa
- : 10 kN/m³;
- \mathrm{\gamma _m}
- γm
- : 70 kN/m³;
- A: 400 cm²;
- p2: 20 kPa;
- g: 10 m/s².
ESQUEMA DO EXERCÍCIO 2
Resolução
Inicialmente, iremos demarcar na figura os pontos notáveis que iremos utilizar durante a questão para mais fácil entendimento no decorrer da mesma.
Os pontos foram escolhidos por serem pontos de mudança de fluido (água e fluido manométrico) ou por serem pontos que se sabe características como velocidade e pressão.
Logo, temos o seguinte esquema:
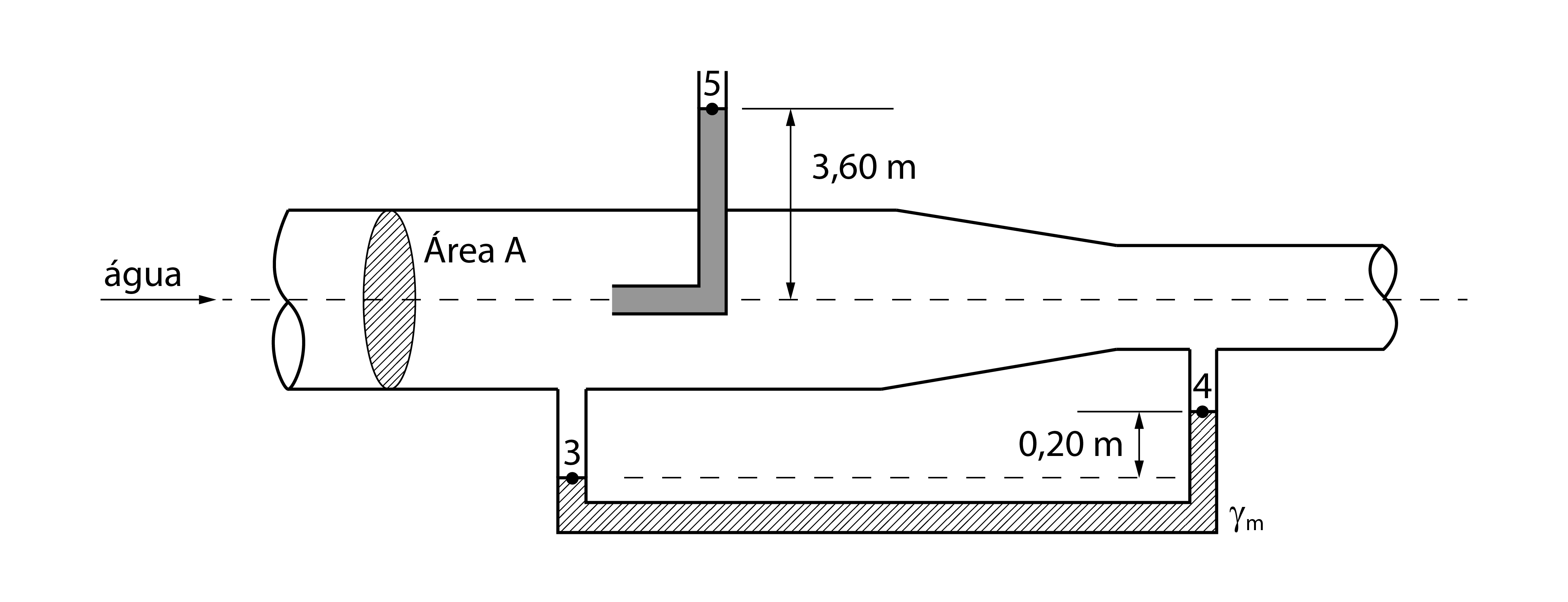
ESQUEMA PARA RESOLUÇÃO DO EXERCÍCIO 2
A questão pede que se determine a vazão do escoamento, ou seja, precisamos determinar a velocidade de escoamento.
Então, vamos aplicar a equação de Bernoulli para os pontos 1 e 5 do escoamento. Temos:
\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = {z_5} + \dfrac{{v_5^2}}{{2 \cdot g}} + \dfrac{{{p_5}}}{{{\gamma _a}}}}
z1
+2⋅g
v1
2
+γa
p1
=z5
+2⋅g
v5
2
+γa
p5
Como o ponto 5 possui velocidade nula, nele atua somente a pressão atmosférica e ele encontra-se numa cota 3,60 m acima do ponto 1, podemos desenvolver a equação para:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
Como não temos os valores de v1 e nem de p1, não conseguimos desenvolver, por ora, tal equacionamento.
Porém, temos um tubo U entre os pontos 1 e 2 e foi dada a pressão no ponto 2, então, podemos utilizar a lei de Stevin entre os pontos 1 e 2 para determinarmos a pressão no ponto1 e, finalmente, chegarmos a velocidade nesse ponto. Para isso, faremos uso dos pontos 3 e 4. Temos então:
\mathrm{{p_3} - {p_1} = {\gamma _a} \cdot h}
p3
−p1
=γa
⋅h
\mathrm{{p_4} - {p_3} = - {\gamma _m} \cdot 0,2}
p4
−p3
=−γm
⋅0,2
\mathrm{{p_2} - {p_4} = - {\gamma _a} \cdot \left( {h - 0,2} \right)}
p2
−p4
=−γa
⋅(h−0,2)
Logo, temos que:
\mathrm{{p_2} - {p_1} = - 0,2 \cdot \left( {{\gamma _m} - {\gamma _a}} \right)}
p2
−p1
=−0,2⋅(γm
−γa
)
Como foram dados que p2 é 20 kPa, \mathrm{\gamma _a}
γa
é 10 kN/m³ e \mathrm{\gamma _m}
γm
é 70 kN/m³, temos:
\mathrm{{p_1} = 32 kPa}
p1
=32kPa
Então, voltando para formulação encontrada no início da questão, temos:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{3,2 \cdot {{10}^4}}}{{10 \cdot {{10}^3}}} = 3,60m}
2⋅g
v1
2
+10⋅103
3,2⋅104
=3,60m
\mathrm{v_1^2 = 0,4 \cdot 2 \cdot 10}
v1
2
=0,4⋅2⋅10
\mathrm{{v_1} = 2,83m/s}
v1
=2,83m/s
Logo, a vazão do escoamento será:
\mathrm{Q = {v_1} \cdot A}
Q=v1
⋅A
\mathrm{Q = 2,83 \cdot 400 \cdot {10^{ - 4}}}
Q=2,83⋅400⋅10−4
\mathbf{Q = 0,1132{m^3}/s}
Q=0,1132m3
/s
Exercício 3
De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de 1,0 mH2O. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto S do sifão deve ser maior que – 60 kPa em pressão relativa e desprezando as perdas de carga determine a velocidade do fluido no sifão e a máxima altura que o ponto S pode ter em relação ao ponto A.
ESQUEMA DO EXERCÍCIO 1
Resolução
Para a resolução da questão, vamos inicialmente determinar a velocidade de fluxo no sifão.
Sabendo que a velocidade de escoamento em todo o sifão é a mesma, podemos utilizar a equação de Bernoulli entre os pontos A e B para determinar tal velocidade. Temos então que:
\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma }}
zA
+2⋅g
vA
2
+γ
pA
=zB
+2⋅g
vB
2
+γ
pB
Como temos que a pressão em ambos os pontos é a própria pressão atmosférica e que a velocidade no ponto A é nula, temos:
\mathrm{{z_A} = \dfrac{{v_B^2}}{{2 \cdot g}}}
zA
=2⋅g
vB
2
\mathbf{{v_B} = 5,66m/s}
vB
=5,66m/s
Agora que já temos o valor da velocidade do fluxo no sifão, podemos aplicar a equação de Bernoulli entre os pontos A e S.
Como temos que a pressão mínima no ponto S é -60 kPa e considerando agora o plano horizontal de referência passando pelo ponto A, temos:
\mathrm{0 = {z_S} + \dfrac{{5,{{66}^2}}}{{2 \cdot g}} - \dfrac{{60 \cdot {{10}^3}}}{{{{10}^4}}}}
0=zS
+2⋅g
5,662
−104
60⋅103
\mathbf{{z_S} = 4,4m}
zS
=4,4m
Exercício 2
Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:
- \mathrm{\gamma _a}
- γa
- : 10 kN/m³;
- \mathrm{\gamma _m}
- γm
- : 70 kN/m³;
- A: 400 cm²;
- p2: 20 kPa;
- g: 10 m/s².
ESQUEMA DO EXERCÍCIO 2
Resolução
Inicialmente, iremos demarcar na figura os pontos notáveis que iremos utilizar durante a questão para mais fácil entendimento no decorrer da mesma.
Os pontos foram escolhidos por serem pontos de mudança de fluido (água e fluido manométrico) ou por serem pontos que se sabe características como velocidade e pressão.
Logo, temos o seguinte esquema:
ESQUEMA PARA RESOLUÇÃO DO EXERCÍCIO 2
A questão pede que se determine a vazão do escoamento, ou seja, precisamos determinar a velocidade de escoamento.
Então, vamos aplicar a equação de Bernoulli para os pontos 1 e 5 do escoamento. Temos:
\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = {z_5} + \dfrac{{v_5^2}}{{2 \cdot g}} + \dfrac{{{p_5}}}{{{\gamma _a}}}}
z1
+2⋅g
v1
2
+γa
p1
=z5
+2⋅g
v5
2
+γa
p5
Como o ponto 5 possui velocidade nula, nele atua somente a pressão atmosférica e ele encontra-se numa cota 3,60 m acima do ponto 1, podemos desenvolver a equação para:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
Como não temos os valores de v1 e nem de p1, não conseguimos desenvolver, por ora, tal equacionamento.
Porém, temos um tubo U entre os pontos 1 e 2 e foi dada a pressão no ponto 2, então, podemos utilizar a lei de Stevin entre os pontos 1 e 2 para determinarmos a pressão no ponto1 e, finalmente, chegarmos a velocidade nesse ponto. Para isso, faremos uso dos pontos 3 e 4. Temos então:
\mathrm{{p_3} - {p_1} = {\gamma _a} \cdot h}
p3
−p1
=γa
⋅h
\mathrm{{p_4} - {p_3} = - {\gamma _m} \cdot 0,2}
p4
−p3
=−γm
⋅0,2
\mathrm{{p_2} - {p_4} = - {\gamma _a} \cdot \left( {h - 0,2} \right)}
p2
−p4
=−γa
⋅(h−0,2)
Logo, temos que:
\mathrm{{p_2} - {p_1} = - 0,2 \cdot \left( {{\gamma _m} - {\gamma _a}} \right)}
p2
−p1
=−0,2⋅(γm
−γa
)
Como foram dados que p2 é 20 kPa, \mathrm{\gamma _a}
γa
é 10 kN/m³ e \mathrm{\gamma _m}
γm
é 70 kN/m³, temos:
\mathrm{{p_1} = 32 kPa}
p1
=32kPa
Então, voltando para formulação encontrada no início da questão, temos:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{3,2 \cdot {{10}^4}}}{{10 \cdot {{10}^3}}} = 3,60m}
2⋅g
v1
2
+10⋅103
3,2⋅104
=3,60m
\mathrm{v_1^2 = 0,4 \cdot 2 \cdot 10}
v1
2
=0,4⋅2⋅10
\mathrm{{v_1} = 2,83m/s}
v1
=2,83m/s
Logo, a vazão do escoamento será:
\mathrm{Q = {v_1} \cdot A}
Q=v1
⋅A
\mathrm{Q = 2,83 \cdot 400 \cdot {10^{ - 4}}}
Q=2,83⋅400⋅10−4
\mathbf{Q = 0,1132{m^3}/s}
Q=0,1132m3
/s
Exercício 3
De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de 1,0 mH2O. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto S do sifão deve ser maior que – 60 kPa em pressão relativa e desprezando as perdas de carga determine a velocidade do fluido no sifão e a máxima altura que o ponto S pode ter em relação ao ponto A.
ESQUEMA DO EXERCÍCIO 1
Resolução
Para a resolução da questão, vamos inicialmente determinar a velocidade de fluxo no sifão.
Sabendo que a velocidade de escoamento em todo o sifão é a mesma, podemos utilizar a equação de Bernoulli entre os pontos A e B para determinar tal velocidade. Temos então que:
\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma }}
zA
+2⋅g
vA
2
+γ
pA
=zB
+2⋅g
vB
2
+γ
pB
Como temos que a pressão em ambos os pontos é a própria pressão atmosférica e que a velocidade no ponto A é nula, temos:
\mathrm{{z_A} = \dfrac{{v_B^2}}{{2 \cdot g}}}
zA
=2⋅g
vB
2
\mathbf{{v_B} = 5,66m/s}
vB
=5,66m/s
Agora que já temos o valor da velocidade do fluxo no sifão, podemos aplicar a equação de Bernoulli entre os pontos A e S.
Como temos que a pressão mínima no ponto S é -60 kPa e considerando agora o plano horizontal de referência passando pelo ponto A, temos:
\mathrm{0 = {z_S} + \dfrac{{5,{{66}^2}}}{{2 \cdot g}} - \dfrac{{60 \cdot {{10}^3}}}{{{{10}^4}}}}
0=zS
+2⋅g
5,662
−104
60⋅103
\mathbf{{z_S} = 4,4m}
zS
=4,4m
Exercício 2
Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:
- \mathrm{\gamma _a}
- γa
- : 10 kN/m³;
- \mathrm{\gamma _m}
- γm
- : 70 kN/m³;
- A: 400 cm²;
- p2: 20 kPa;
- g: 10 m/s².
ESQUEMA DO EXERCÍCIO 2
Resolução
Inicialmente, iremos demarcar na figura os pontos notáveis que iremos utilizar durante a questão para mais fácil entendimento no decorrer da mesma.
Os pontos foram escolhidos por serem pontos de mudança de fluido (água e fluido manométrico) ou por serem pontos que se sabe características como velocidade e pressão.
Logo, temos o seguinte esquema:
ESQUEMA PARA RESOLUÇÃO DO EXERCÍCIO 2
A questão pede que se determine a vazão do escoamento, ou seja, precisamos determinar a velocidade de escoamento.
Então, vamos aplicar a equação de Bernoulli para os pontos 1 e 5 do escoamento. Temos:
\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = {z_5} + \dfrac{{v_5^2}}{{2 \cdot g}} + \dfrac{{{p_5}}}{{{\gamma _a}}}}
z1
+2⋅g
v1
2
+γa
p1
=z5
+2⋅g
v5
2
+γa
p5
Como o ponto 5 possui velocidade nula, nele atua somente a pressão atmosférica e ele encontra-se numa cota 3,60 m acima do ponto 1, podemos desenvolver a equação para:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
Como não temos os valores de v1 e nem de p1, não conseguimos desenvolver, por ora, tal equacionamento.
Porém, temos um tubo U entre os pontos 1 e 2 e foi dada a pressão no ponto 2, então, podemos utilizar a lei de Stevin entre os pontos 1 e 2 para determinarmos a pressão no ponto1 e, finalmente, chegarmos a velocidade nesse ponto. Para isso, faremos uso dos pontos 3 e 4. Temos então:
\mathrm{{p_3} - {p_1} = {\gamma _a} \cdot h}
p3
−p1
=γa
⋅h
\mathrm{{p_4} - {p_3} = - {\gamma _m} \cdot 0,2}
p4
−p3
=−γm
⋅0,2
\mathrm{{p_2} - {p_4} = - {\gamma _a} \cdot \left( {h - 0,2} \right)}
p2
−p4
=−γa
⋅(h−0,2)
Logo, temos que:
\mathrm{{p_2} - {p_1} = - 0,2 \cdot \left( {{\gamma _m} - {\gamma _a}} \right)}
p2
−p1
=−0,2⋅(γm
−γa
)
Como foram dados que p2 é 20 kPa, \mathrm{\gamma _a}
γa
é 10 kN/m³ e \mathrm{\gamma _m}
γm
é 70 kN/m³, temos:
\mathrm{{p_1} = 32 kPa}
p1
=32kPa
Então, voltando para formulação encontrada no início da questão, temos:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{3,2 \cdot {{10}^4}}}{{10 \cdot {{10}^3}}} = 3,60m}
2⋅g
v1
2
+10⋅103
3,2⋅104
=3,60m
\mathrm{v_1^2 = 0,4 \cdot 2 \cdot 10}
v1
2
=0,4⋅2⋅10
\mathrm{{v_1} = 2,83m/s}
v1
=2,83m/s
Logo, a vazão do escoamento será:
\mathrm{Q = {v_1} \cdot A}
Q=v1
⋅A
\mathrm{Q = 2,83 \cdot 400 \cdot {10^{ - 4}}}
Q=2,83⋅400⋅10−4
\mathbf{Q = 0,1132{m^3}/s}
Q=0,1132m3
/s
Exercício 3
De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de 1,0 mH2O. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto S do sifão deve ser maior que – 60 kPa em pressão relativa e desprezando as perdas de carga determine a velocidade do fluido no sifão e a máxima altura que o ponto S pode ter em relação ao ponto A.
ESQUEMA DO EXERCÍCIO 1
Resolução
Para a resolução da questão, vamos inicialmente determinar a velocidade de fluxo no sifão.
Sabendo que a velocidade de escoamento em todo o sifão é a mesma, podemos utilizar a equação de Bernoulli entre os pontos A e B para determinar tal velocidade. Temos então que:
\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma }}
zA
+2⋅g
vA
2
+γ
pA
=zB
+2⋅g
vB
2
+γ
pB
Como temos que a pressão em ambos os pontos é a própria pressão atmosférica e que a velocidade no ponto A é nula, temos:
\mathrm{{z_A} = \dfrac{{v_B^2}}{{2 \cdot g}}}
zA
=2⋅g
vB
2
\mathbf{{v_B} = 5,66m/s}
vB
=5,66m/s
Agora que já temos o valor da velocidade do fluxo no sifão, podemos aplicar a equação de Bernoulli entre os pontos A e S.
Como temos que a pressão mínima no ponto S é -60 kPa e considerando agora o plano horizontal de referência passando pelo ponto A, temos:
\mathrm{0 = {z_S} + \dfrac{{5,{{66}^2}}}{{2 \cdot g}} - \dfrac{{60 \cdot {{10}^3}}}{{{{10}^4}}}}
0=zS
+2⋅g
5,662
−104
60⋅103
\mathbf{{z_S} = 4,4m}
zS
=4,4m
Exercício 2
Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:
- \mathrm{\gamma _a}
- γa
- : 10 kN/m³;
- \mathrm{\gamma _m}
- γm
- : 70 kN/m³;
- A: 400 cm²;
- p2: 20 kPa;
- g: 10 m/s².
ESQUEMA DO EXERCÍCIO 2
Resolução
Inicialmente, iremos demarcar na figura os pontos notáveis que iremos utilizar durante a questão para mais fácil entendimento no decorrer da mesma.
Os pontos foram escolhidos por serem pontos de mudança de fluido (água e fluido manométrico) ou por serem pontos que se sabe características como velocidade e pressão.
Logo, temos o seguinte esquema:
ESQUEMA PARA RESOLUÇÃO DO EXERCÍCIO 2
A questão pede que se determine a vazão do escoamento, ou seja, precisamos determinar a velocidade de escoamento.
Então, vamos aplicar a equação de Bernoulli para os pontos 1 e 5 do escoamento. Temos:
\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = {z_5} + \dfrac{{v_5^2}}{{2 \cdot g}} + \dfrac{{{p_5}}}{{{\gamma _a}}}}
z1
+2⋅g
v1
2
+γa
p1
=z5
+2⋅g
v5
2
+γa
p5
Como o ponto 5 possui velocidade nula, nele atua somente a pressão atmosférica e ele encontra-se numa cota 3,60 m acima do ponto 1, podemos desenvolver a equação para:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
Como não temos os valores de v1 e nem de p1, não conseguimos desenvolver, por ora, tal equacionamento.
Porém, temos um tubo U entre os pontos 1 e 2 e foi dada a pressão no ponto 2, então, podemos utilizar a lei de Stevin entre os pontos 1 e 2 para determinarmos a pressão no ponto1 e, finalmente, chegarmos a velocidade nesse ponto. Para isso, faremos uso dos pontos 3 e 4. Temos então:
\mathrm{{p_3} - {p_1} = {\gamma _a} \cdot h}
p3
−p1
=γa
⋅h
\mathrm{{p_4} - {p_3} = - {\gamma _m} \cdot 0,2}
p4
−p3
=−γm
⋅0,2
\mathrm{{p_2} - {p_4} = - {\gamma _a} \cdot \left( {h - 0,2} \right)}
p2
−p4
=−γa
⋅(h−0,2)
Logo, temos que:
\mathrm{{p_2} - {p_1} = - 0,2 \cdot \left( {{\gamma _m} - {\gamma _a}} \right)}
p2
−p1
=−0,2⋅(γm
−γa
)
Como foram dados que p2 é 20 kPa, \mathrm{\gamma _a}
γa
é 10 kN/m³ e \mathrm{\gamma _m}
γm
é 70 kN/m³, temos:
\mathrm{{p_1} = 32 kPa}
p1
=32kPa
Então, voltando para formulação encontrada no início da questão, temos:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{3,2 \cdot {{10}^4}}}{{10 \cdot {{10}^3}}} = 3,60m}
2⋅g
v1
2
+10⋅103
3,2⋅104
=3,60m
\mathrm{v_1^2 = 0,4 \cdot 2 \cdot 10}
v1
2
=0,4⋅2⋅10
\mathrm{{v_1} = 2,83m/s}
v1
=2,83m/s
Logo, a vazão do escoamento será:
\mathrm{Q = {v_1} \cdot A}
Q=v1
⋅A
\mathrm{Q = 2,83 \cdot 400 \cdot {10^{ - 4}}}
Q=2,83⋅400⋅10−4
\mathbf{Q = 0,1132{m^3}/s}
Q=0,1132m3
/s
Exercício 3
De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de 1,0 mH2O. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto S do sifão deve ser maior que – 60 kPa em pressão relativa e desprezando as perdas de carga determine a velocidade do fluido no sifão e a máxima altura que o ponto S pode ter em relação ao ponto A.
ESQUEMA DO EXERCÍCIO 1
Resolução
Para a resolução da questão, vamos inicialmente determinar a velocidade de fluxo no sifão.
Sabendo que a velocidade de escoamento em todo o sifão é a mesma, podemos utilizar a equação de Bernoulli entre os pontos A e B para determinar tal velocidade. Temos então que:
\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma }}
zA
+2⋅g
vA
2
+γ
pA
=zB
+2⋅g
vB
2
+γ
pB
Como temos que a pressão em ambos os pontos é a própria pressão atmosférica e que a velocidade no ponto A é nula, temos:
\mathrm{{z_A} = \dfrac{{v_B^2}}{{2 \cdot g}}}
zA
=2⋅g
vB
2
\mathbf{{v_B} = 5,66m/s}
vB
=5,66m/s
Agora que já temos o valor da velocidade do fluxo no sifão, podemos aplicar a equação de Bernoulli entre os pontos A e S.
Como temos que a pressão mínima no ponto S é -60 kPa e considerando agora o plano horizontal de referência passando pelo ponto A, temos:
\mathrm{0 = {z_S} + \dfrac{{5,{{66}^2}}}{{2 \cdot g}} - \dfrac{{60 \cdot {{10}^3}}}{{{{10}^4}}}}
0=zS
+2⋅g
5,662
−104
60⋅103
\mathbf{{z_S} = 4,4m}
zS
=4,4m
Exercício 2
Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:
- \mathrm{\gamma _a}
- γa
- : 10 kN/m³;
- \mathrm{\gamma _m}
- γm
- : 70 kN/m³;
- A: 400 cm²;
- p2: 20 kPa;
- g: 10 m/s².
ESQUEMA DO EXERCÍCIO 2
Resolução
Inicialmente, iremos demarcar na figura os pontos notáveis que iremos utilizar durante a questão para mais fácil entendimento no decorrer da mesma.
Os pontos foram escolhidos por serem pontos de mudança de fluido (água e fluido manométrico) ou por serem pontos que se sabe características como velocidade e pressão.
Logo, temos o seguinte esquema:
ESQUEMA PARA RESOLUÇÃO DO EXERCÍCIO 2
A questão pede que se determine a vazão do escoamento, ou seja, precisamos determinar a velocidade de escoamento.
Então, vamos aplicar a equação de Bernoulli para os pontos 1 e 5 do escoamento. Temos:
\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = {z_5} + \dfrac{{v_5^2}}{{2 \cdot g}} + \dfrac{{{p_5}}}{{{\gamma _a}}}}
z1
+2⋅g
v1
2
+γa
p1
=z5
+2⋅g
v5
2
+γa
p5
Como o ponto 5 possui velocidade nula, nele atua somente a pressão atmosférica e ele encontra-se numa cota 3,60 m acima do ponto 1, podemos desenvolver a equação para:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
Como não temos os valores de v1 e nem de p1, não conseguimos desenvolver, por ora, tal equacionamento.
Porém, temos um tubo U entre os pontos 1 e 2 e foi dada a pressão no ponto 2, então, podemos utilizar a lei de Stevin entre os pontos 1 e 2 para determinarmos a pressão no ponto1 e, finalmente, chegarmos a velocidade nesse ponto. Para isso, faremos uso dos pontos 3 e 4. Temos então:
\mathrm{{p_3} - {p_1} = {\gamma _a} \cdot h}
p3
−p1
=γa
⋅h
\mathrm{{p_4} - {p_3} = - {\gamma _m} \cdot 0,2}
p4
−p3
=−γm
⋅0,2
\mathrm{{p_2} - {p_4} = - {\gamma _a} \cdot \left( {h - 0,2} \right)}
p2
−p4
=−γa
⋅(h−0,2)
Logo, temos que:
\mathrm{{p_2} - {p_1} = - 0,2 \cdot \left( {{\gamma _m} - {\gamma _a}} \right)}
p2
−p1
=−0,2⋅(γm
−γa
)
Como foram dados que p2 é 20 kPa, \mathrm{\gamma _a}
γa
é 10 kN/m³ e \mathrm{\gamma _m}
γm
é 70 kN/m³, temos:
\mathrm{{p_1} = 32 kPa}
p1
=32kPa
Então, voltando para formulação encontrada no início da questão, temos:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{3,2 \cdot {{10}^4}}}{{10 \cdot {{10}^3}}} = 3,60m}
2⋅g
v1
2
+10⋅103
3,2⋅104
=3,60m
\mathrm{v_1^2 = 0,4 \cdot 2 \cdot 10}
v1
2
=0,4⋅2⋅10
\mathrm{{v_1} = 2,83m/s}
v1
=2,83m/s
Logo, a vazão do escoamento será:
\mathrm{Q = {v_1} \cdot A}
Q=v1
⋅A
\mathrm{Q = 2,83 \cdot 400 \cdot {10^{ - 4}}}
Q=2,83⋅400⋅10−4
\mathbf{Q = 0,1132{m^3}/s}
Q=0,1132m3
/s
Exercício 3
De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de 1,0 mH2O. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto S do sifão deve ser maior que – 60 kPa em pressão relativa e desprezando as perdas de carga determine a velocidade do fluido no sifão e a máxima altura que o ponto S pode ter em relação ao ponto A.
ESQUEMA DO EXERCÍCIO 1
Resolução
Para a resolução da questão, vamos inicialmente determinar a velocidade de fluxo no sifão.
Sabendo que a velocidade de escoamento em todo o sifão é a mesma, podemos utilizar a equação de Bernoulli entre os pontos A e B para determinar tal velocidade. Temos então que:
\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma }}
zA
+2⋅g
vA
2
+γ
pA
=zB
+2⋅g
vB
2
+γ
pB
Como temos que a pressão em ambos os pontos é a própria pressão atmosférica e que a velocidade no ponto A é nula, temos:
\mathrm{{z_A} = \dfrac{{v_B^2}}{{2 \cdot g}}}
zA
=2⋅g
vB
2
\mathbf{{v_B} = 5,66m/s}
vB
=5,66m/s
Agora que já temos o valor da velocidade do fluxo no sifão, podemos aplicar a equação de Bernoulli entre os pontos A e S.
Como temos que a pressão mínima no ponto S é -60 kPa e considerando agora o plano horizontal de referência passando pelo ponto A, temos:
\mathrm{0 = {z_S} + \dfrac{{5,{{66}^2}}}{{2 \cdot g}} - \dfrac{{60 \cdot {{10}^3}}}{{{{10}^4}}}}
0=zS
+2⋅g
5,662
−104
60⋅103
\mathbf{{z_S} = 4,4m}
zS
=4,4m
Exercício 2
Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:
- \mathrm{\gamma _a}
- γa
- : 10 kN/m³;
- \mathrm{\gamma _m}
- γm
- : 70 kN/m³;
- A: 400 cm²;
- p2: 20 kPa;
- g: 10 m/s².
ESQUEMA DO EXERCÍCIO 2
Resolução
Inicialmente, iremos demarcar na figura os pontos notáveis que iremos utilizar durante a questão para mais fácil entendimento no decorrer da mesma.
Os pontos foram escolhidos por serem pontos de mudança de fluido (água e fluido manométrico) ou por serem pontos que se sabe características como velocidade e pressão.
Logo, temos o seguinte esquema:
ESQUEMA PARA RESOLUÇÃO DO EXERCÍCIO 2
A questão pede que se determine a vazão do escoamento, ou seja, precisamos determinar a velocidade de escoamento.
Então, vamos aplicar a equação de Bernoulli para os pontos 1 e 5 do escoamento. Temos:
\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = {z_5} + \dfrac{{v_5^2}}{{2 \cdot g}} + \dfrac{{{p_5}}}{{{\gamma _a}}}}
z1
+2⋅g
v1
2
+γa
p1
=z5
+2⋅g
v5
2
+γa
p5
Como o ponto 5 possui velocidade nula, nele atua somente a pressão atmosférica e ele encontra-se numa cota 3,60 m acima do ponto 1, podemos desenvolver a equação para:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
Como não temos os valores de v1 e nem de p1, não conseguimos desenvolver, por ora, tal equacionamento.
Porém, temos um tubo U entre os pontos 1 e 2 e foi dada a pressão no ponto 2, então, podemos utilizar a lei de Stevin entre os pontos 1 e 2 para determinarmos a pressão no ponto1 e, finalmente, chegarmos a velocidade nesse ponto. Para isso, faremos uso dos pontos 3 e 4. Temos então:
\mathrm{{p_3} - {p_1} = {\gamma _a} \cdot h}
p3
−p1
=γa
⋅h
\mathrm{{p_4} - {p_3} = - {\gamma _m} \cdot 0,2}
p4
−p3
=−γm
⋅0,2
\mathrm{{p_2} - {p_4} = - {\gamma _a} \cdot \left( {h - 0,2} \right)}
p2
−p4
=−γa
⋅(h−0,2)
Logo, temos que:
\mathrm{{p_2} - {p_1} = - 0,2 \cdot \left( {{\gamma _m} - {\gamma _a}} \right)}
p2
−p1
=−0,2⋅(γm
−γa
)
Como foram dados que p2 é 20 kPa, \mathrm{\gamma _a}
γa
é 10 kN/m³ e \mathrm{\gamma _m}
γm
é 70 kN/m³, temos:
\mathrm{{p_1} = 32 kPa}
p1
=32kPa
Então, voltando para formulação encontrada no início da questão, temos:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{3,2 \cdot {{10}^4}}}{{10 \cdot {{10}^3}}} = 3,60m}
2⋅g
v1
2
+10⋅103
3,2⋅104
=3,60m
\mathrm{v_1^2 = 0,4 \cdot 2 \cdot 10}
v1
2
=0,4⋅2⋅10
\mathrm{{v_1} = 2,83m/s}
v1
=2,83m/s
Logo, a vazão do escoamento será:
\mathrm{Q = {v_1} \cdot A}
Q=v1
⋅A
\mathrm{Q = 2,83 \cdot 400 \cdot {10^{ - 4}}}
Q=2,83⋅400⋅10−4
\mathbf{Q = 0,1132{m^3}/s}
Q=0,1132m3
/s
Exercício 3
De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de 1,0 mH2O. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto S do sifão deve ser maior que – 60 kPa em pressão relativa e desprezando as perdas de carga determine a velocidade do fluido no sifão e a máxima altura que o ponto S pode ter em relação ao ponto A.
ESQUEMA DO EXERCÍCIO 1
Resolução
Para a resolução da questão, vamos inicialmente determinar a velocidade de fluxo no sifão.
Sabendo que a velocidade de escoamento em todo o sifão é a mesma, podemos utilizar a equação de Bernoulli entre os pontos A e B para determinar tal velocidade. Temos então que:
\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma }}
zA
+2⋅g
vA
2
+γ
pA
=zB
+2⋅g
vB
2
+γ
pB
Como temos que a pressão em ambos os pontos é a própria pressão atmosférica e que a velocidade no ponto A é nula, temos:
\mathrm{{z_A} = \dfrac{{v_B^2}}{{2 \cdot g}}}
zA
=2⋅g
vB
2
\mathbf{{v_B} = 5,66m/s}
vB
=5,66m/s
Agora que já temos o valor da velocidade do fluxo no sifão, podemos aplicar a equação de Bernoulli entre os pontos A e S.
Como temos que a pressão mínima no ponto S é -60 kPa e considerando agora o plano horizontal de referência passando pelo ponto A, temos:
\mathrm{0 = {z_S} + \dfrac{{5,{{66}^2}}}{{2 \cdot g}} - \dfrac{{60 \cdot {{10}^3}}}{{{{10}^4}}}}
0=zS
+2⋅g
5,662
−104
60⋅103
\mathbf{{z_S} = 4,4m}
zS
=4,4m
Exercício 2
Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:
- \mathrm{\gamma _a}
- γa
- : 10 kN/m³;
- \mathrm{\gamma _m}
- γm
- : 70 kN/m³;
- A: 400 cm²;
- p2: 20 kPa;
- g: 10 m/s².
ESQUEMA DO EXERCÍCIO 2
Resolução
Inicialmente, iremos demarcar na figura os pontos notáveis que iremos utilizar durante a questão para mais fácil entendimento no decorrer da mesma.
Os pontos foram escolhidos por serem pontos de mudança de fluido (água e fluido manométrico) ou por serem pontos que se sabe características como velocidade e pressão.
Logo, temos o seguinte esquema:
ESQUEMA PARA RESOLUÇÃO DO EXERCÍCIO 2
A questão pede que se determine a vazão do escoamento, ou seja, precisamos determinar a velocidade de escoamento.
Então, vamos aplicar a equação de Bernoulli para os pontos 1 e 5 do escoamento. Temos:
\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = {z_5} + \dfrac{{v_5^2}}{{2 \cdot g}} + \dfrac{{{p_5}}}{{{\gamma _a}}}}
z1
+2⋅g
v1
2
+γa
p1
=z5
+2⋅g
v5
2
+γa
p5
Como o ponto 5 possui velocidade nula, nele atua somente a pressão atmosférica e ele encontra-se numa cota 3,60 m acima do ponto 1, podemos desenvolver a equação para:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
Como não temos os valores de v1 e nem de p1, não conseguimos desenvolver, por ora, tal equacionamento.
Porém, temos um tubo U entre os pontos 1 e 2 e foi dada a pressão no ponto 2, então, podemos utilizar a lei de Stevin entre os pontos 1 e 2 para determinarmos a pressão no ponto1 e, finalmente, chegarmos a velocidade nesse ponto. Para isso, faremos uso dos pontos 3 e 4. Temos então:
\mathrm{{p_3} - {p_1} = {\gamma _a} \cdot h}
p3
−p1
=γa
⋅h
\mathrm{{p_4} - {p_3} = - {\gamma _m} \cdot 0,2}
p4
−p3
=−γm
⋅0,2
\mathrm{{p_2} - {p_4} = - {\gamma _a} \cdot \left( {h - 0,2} \right)}
p2
−p4
=−γa
⋅(h−0,2)
Logo, temos que:
\mathrm{{p_2} - {p_1} = - 0,2 \cdot \left( {{\gamma _m} - {\gamma _a}} \right)}
p2
−p1
=−0,2⋅(γm
−γa
)
Como foram dados que p2 é 20 kPa, \mathrm{\gamma _a}
γa
é 10 kN/m³ e \mathrm{\gamma _m}
γm
é 70 kN/m³, temos:
\mathrm{{p_1} = 32 kPa}
p1
=32kPa
Então, voltando para formulação encontrada no início da questão, temos:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{3,2 \cdot {{10}^4}}}{{10 \cdot {{10}^3}}} = 3,60m}
2⋅g
v1
2
+10⋅103
3,2⋅104
=3,60m
\mathrm{v_1^2 = 0,4 \cdot 2 \cdot 10}
v1
2
=0,4⋅2⋅10
\mathrm{{v_1} = 2,83m/s}
v1
=2,83m/s
Logo, a vazão do escoamento será:
\mathrm{Q = {v_1} \cdot A}
Q=v1
⋅A
\mathrm{Q = 2,83 \cdot 400 \cdot {10^{ - 4}}}
Q=2,83⋅400⋅10−4
\mathbf{Q = 0,1132{m^3}/s}
Q=0,1132m3
/s
Exercício 3
De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de 1,0 mH2O. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto S do sifão deve ser maior que – 60 kPa em pressão relativa e desprezando as perdas de carga determine a velocidade do fluido no sifão e a máxima altura que o ponto S pode ter em relação ao ponto A.
ESQUEMA DO EXERCÍCIO 1
Resolução
Para a resolução da questão, vamos inicialmente determinar a velocidade de fluxo no sifão.
Sabendo que a velocidade de escoamento em todo o sifão é a mesma, podemos utilizar a equação de Bernoulli entre os pontos A e B para determinar tal velocidade. Temos então que:
\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma }}
zA
+2⋅g
vA
2
+γ
pA
=zB
+2⋅g
vB
2
+γ
pB
Como temos que a pressão em ambos os pontos é a própria pressão atmosférica e que a velocidade no ponto A é nula, temos:
\mathrm{{z_A} = \dfrac{{v_B^2}}{{2 \cdot g}}}
zA
=2⋅g
vB
2
\mathbf{{v_B} = 5,66m/s}
vB
=5,66m/s
Agora que já temos o valor da velocidade do fluxo no sifão, podemos aplicar a equação de Bernoulli entre os pontos A e S.
Como temos que a pressão mínima no ponto S é -60 kPa e considerando agora o plano horizontal de referência passando pelo ponto A, temos:
\mathrm{0 = {z_S} + \dfrac{{5,{{66}^2}}}{{2 \cdot g}} - \dfrac{{60 \cdot {{10}^3}}}{{{{10}^4}}}}
0=zS
+2⋅g
5,662
−104
60⋅103
\mathbf{{z_S} = 4,4m}
zS
=4,4m
Exercício 2
Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:
- \mathrm{\gamma _a}
- γa
- : 10 kN/m³;
- \mathrm{\gamma _m}
- γm
- : 70 kN/m³;
- A: 400 cm²;
- p2: 20 kPa;
- g: 10 m/s².
ESQUEMA DO EXERCÍCIO 2
Resolução
Inicialmente, iremos demarcar na figura os pontos notáveis que iremos utilizar durante a questão para mais fácil entendimento no decorrer da mesma.
Os pontos foram escolhidos por serem pontos de mudança de fluido (água e fluido manométrico) ou por serem pontos que se sabe características como velocidade e pressão.
Logo, temos o seguinte esquema:
ESQUEMA PARA RESOLUÇÃO DO EXERCÍCIO 2
A questão pede que se determine a vazão do escoamento, ou seja, precisamos determinar a velocidade de escoamento.
Então, vamos aplicar a equação de Bernoulli para os pontos 1 e 5 do escoamento. Temos:
\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = {z_5} + \dfrac{{v_5^2}}{{2 \cdot g}} + \dfrac{{{p_5}}}{{{\gamma _a}}}}
z1
+2⋅g
v1
2
+γa
p1
=z5
+2⋅g
v5
2
+γa
p5
Como o ponto 5 possui velocidade nula, nele atua somente a pressão atmosférica e ele encontra-se numa cota 3,60 m acima do ponto 1, podemos desenvolver a equação para:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
Como não temos os valores de v1 e nem de p1, não conseguimos desenvolver, por ora, tal equacionamento.
Porém, temos um tubo U entre os pontos 1 e 2 e foi dada a pressão no ponto 2, então, podemos utilizar a lei de Stevin entre os pontos 1 e 2 para determinarmos a pressão no ponto1 e, finalmente, chegarmos a velocidade nesse ponto. Para isso, faremos uso dos pontos 3 e 4. Temos então:
\mathrm{{p_3} - {p_1} = {\gamma _a} \cdot h}
p3
−p1
=γa
⋅h
\mathrm{{p_4} - {p_3} = - {\gamma _m} \cdot 0,2}
p4
−p3
=−γm
⋅0,2
\mathrm{{p_2} - {p_4} = - {\gamma _a} \cdot \left( {h - 0,2} \right)}
p2
−p4
=−γa
⋅(h−0,2)
Logo, temos que:
\mathrm{{p_2} - {p_1} = - 0,2 \cdot \left( {{\gamma _m} - {\gamma _a}} \right)}
p2
−p1
=−0,2⋅(γm
−γa
)
Como foram dados que p2 é 20 kPa, \mathrm{\gamma _a}
γa
é 10 kN/m³ e \mathrm{\gamma _m}
γm
é 70 kN/m³, temos:
\mathrm{{p_1} = 32 kPa}
p1
=32kPa
Então, voltando para formulação encontrada no início da questão, temos:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{3,2 \cdot {{10}^4}}}{{10 \cdot {{10}^3}}} = 3,60m}
2⋅g
v1
2
+10⋅103
3,2⋅104
=3,60m
\mathrm{v_1^2 = 0,4 \cdot 2 \cdot 10}
v1
2
=0,4⋅2⋅10
\mathrm{{v_1} = 2,83m/s}
v1
=2,83m/s
Logo, a vazão do escoamento será:
\mathrm{Q = {v_1} \cdot A}
Q=v1
⋅A
\mathrm{Q = 2,83 \cdot 400 \cdot {10^{ - 4}}}
Q=2,83⋅400⋅10−4
\mathbf{Q = 0,1132{m^3}/s}
Q=0,1132m3
/s
Exercício 3
De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de 1,0 mH2O. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto S do sifão deve ser maior que – 60 kPa em pressão relativa e desprezando as perdas de carga determine a velocidade do fluido no sifão e a máxima altura que o ponto S pode ter em relação ao ponto A.
ESQUEMA DO EXERCÍCIO 1
Resolução
Para a resolução da questão, vamos inicialmente determinar a velocidade de fluxo no sifão.
Sabendo que a velocidade de escoamento em todo o sifão é a mesma, podemos utilizar a equação de Bernoulli entre os pontos A e B para determinar tal velocidade. Temos então que:
\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma }}
zA
+2⋅g
vA
2
+γ
pA
=zB
+2⋅g
vB
2
+γ
pB
Como temos que a pressão em ambos os pontos é a própria pressão atmosférica e que a velocidade no ponto A é nula, temos:
\mathrm{{z_A} = \dfrac{{v_B^2}}{{2 \cdot g}}}
zA
=2⋅g
vB
2
\mathbf{{v_B} = 5,66m/s}
vB
=5,66m/s
Agora que já temos o valor da velocidade do fluxo no sifão, podemos aplicar a equação de Bernoulli entre os pontos A e S.
Como temos que a pressão mínima no ponto S é -60 kPa e considerando agora o plano horizontal de referência passando pelo ponto A, temos:
\mathrm{0 = {z_S} + \dfrac{{5,{{66}^2}}}{{2 \cdot g}} - \dfrac{{60 \cdot {{10}^3}}}{{{{10}^4}}}}
0=zS
+2⋅g
5,662
−104
60⋅103
\mathbf{{z_S} = 4,4m}
zS
=4,4m
Exercício 2
Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:
- \mathrm{\gamma _a}
- γa
- : 10 kN/m³;
- \mathrm{\gamma _m}
- γm
- : 70 kN/m³;
- A: 400 cm²;
- p2: 20 kPa;
- g: 10 m/s².
ESQUEMA DO EXERCÍCIO 2
Resolução
Inicialmente, iremos demarcar na figura os pontos notáveis que iremos utilizar durante a questão para mais fácil entendimento no decorrer da mesma.
Os pontos foram escolhidos por serem pontos de mudança de fluido (água e fluido manométrico) ou por serem pontos que se sabe características como velocidade e pressão.
Logo, temos o seguinte esquema:
ESQUEMA PARA RESOLUÇÃO DO EXERCÍCIO 2
A questão pede que se determine a vazão do escoamento, ou seja, precisamos determinar a velocidade de escoamento.
Então, vamos aplicar a equação de Bernoulli para os pontos 1 e 5 do escoamento. Temos:
\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = {z_5} + \dfrac{{v_5^2}}{{2 \cdot g}} + \dfrac{{{p_5}}}{{{\gamma _a}}}}
z1
+2⋅g
v1
2
+γa
p1
=z5
+2⋅g
v5
2
+γa
p5
Como o ponto 5 possui velocidade nula, nele atua somente a pressão atmosférica e ele encontra-se numa cota 3,60 m acima do ponto 1, podemos desenvolver a equação para:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
Como não temos os valores de v1 e nem de p1, não conseguimos desenvolver, por ora, tal equacionamento.
Porém, temos um tubo U entre os pontos 1 e 2 e foi dada a pressão no ponto 2, então, podemos utilizar a lei de Stevin entre os pontos 1 e 2 para determinarmos a pressão no ponto1 e, finalmente, chegarmos a velocidade nesse ponto. Para isso, faremos uso dos pontos 3 e 4. Temos então:
\mathrm{{p_3} - {p_1} = {\gamma _a} \cdot h}
p3
−p1
=γa
⋅h
\mathrm{{p_4} - {p_3} = - {\gamma _m} \cdot 0,2}
p4
−p3
=−γm
⋅0,2
\mathrm{{p_2} - {p_4} = - {\gamma _a} \cdot \left( {h - 0,2} \right)}
p2
−p4
=−γa
⋅(h−0,2)
Logo, temos que:
\mathrm{{p_2} - {p_1} = - 0,2 \cdot \left( {{\gamma _m} - {\gamma _a}} \right)}
p2
−p1
=−0,2⋅(γm
−γa
)
Como foram dados que p2 é 20 kPa, \mathrm{\gamma _a}
γa
é 10 kN/m³ e \mathrm{\gamma _m}
γm
é 70 kN/m³, temos:
\mathrm{{p_1} = 32 kPa}
p1
=32kPa
Então, voltando para formulação encontrada no início da questão, temos:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{3,2 \cdot {{10}^4}}}{{10 \cdot {{10}^3}}} = 3,60m}
2⋅g
v1
2
+10⋅103
3,2⋅104
=3,60m
\mathrm{v_1^2 = 0,4 \cdot 2 \cdot 10}
v1
2
=0,4⋅2⋅10
\mathrm{{v_1} = 2,83m/s}
v1
=2,83m/s
Logo, a vazão do escoamento será:
\mathrm{Q = {v_1} \cdot A}
Q=v1
⋅A
\mathrm{Q = 2,83 \cdot 400 \cdot {10^{ - 4}}}
Q=2,83⋅400⋅10−4
\mathbf{Q = 0,1132{m^3}/s}
Q=0,1132m3
/s
Exercício 3
De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de 1,0 mH2O. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto S do sifão deve ser maior que – 60 kPa em pressão relativa e desprezando as perdas de carga determine a velocidade do fluido no sifão e a máxima altura que o ponto S pode ter em relação ao ponto A.
ESQUEMA DO EXERCÍCIO 1
Resolução
Para a resolução da questão, vamos inicialmente determinar a velocidade de fluxo no sifão.
Sabendo que a velocidade de escoamento em todo o sifão é a mesma, podemos utilizar a equação de Bernoulli entre os pontos A e B para determinar tal velocidade. Temos então que:
\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma }}
zA
+2⋅g
vA
2
+γ
pA
=zB
+2⋅g
vB
2
+γ
pB
Como temos que a pressão em ambos os pontos é a própria pressão atmosférica e que a velocidade no ponto A é nula, temos:
\mathrm{{z_A} = \dfrac{{v_B^2}}{{2 \cdot g}}}
zA
=2⋅g
vB
2
\mathbf{{v_B} = 5,66m/s}
vB
=5,66m/s
Agora que já temos o valor da velocidade do fluxo no sifão, podemos aplicar a equação de Bernoulli entre os pontos A e S.
Como temos que a pressão mínima no ponto S é -60 kPa e considerando agora o plano horizontal de referência passando pelo ponto A, temos:
\mathrm{0 = {z_S} + \dfrac{{5,{{66}^2}}}{{2 \cdot g}} - \dfrac{{60 \cdot {{10}^3}}}{{{{10}^4}}}}
0=zS
+2⋅g
5,662
−104
60⋅103
\mathbf{{z_S} = 4,4m}
zS
=4,4m
Exercício 2
Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:
- \mathrm{\gamma _a}
- γa
- : 10 kN/m³;
- \mathrm{\gamma _m}
- γm
- : 70 kN/m³;
- A: 400 cm²;
- p2: 20 kPa;
- g: 10 m/s².
ESQUEMA DO EXERCÍCIO 2
Resolução
Inicialmente, iremos demarcar na figura os pontos notáveis que iremos utilizar durante a questão para mais fácil entendimento no decorrer da mesma.
Os pontos foram escolhidos por serem pontos de mudança de fluido (água e fluido manométrico) ou por serem pontos que se sabe características como velocidade e pressão.
Logo, temos o seguinte esquema:
ESQUEMA PARA RESOLUÇÃO DO EXERCÍCIO 2
A questão pede que se determine a vazão do escoamento, ou seja, precisamos determinar a velocidade de escoamento.
Então, vamos aplicar a equação de Bernoulli para os pontos 1 e 5 do escoamento. Temos:
\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = {z_5} + \dfrac{{v_5^2}}{{2 \cdot g}} + \dfrac{{{p_5}}}{{{\gamma _a}}}}
z1
+2⋅g
v1
2
+γa
p1
=z5
+2⋅g
v5
2
+γa
p5
Como o ponto 5 possui velocidade nula, nele atua somente a pressão atmosférica e ele encontra-se numa cota 3,60 m acima do ponto 1, podemos desenvolver a equação para:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
Como não temos os valores de v1 e nem de p1, não conseguimos desenvolver, por ora, tal equacionamento.
Porém, temos um tubo U entre os pontos 1 e 2 e foi dada a pressão no ponto 2, então, podemos utilizar a lei de Stevin entre os pontos 1 e 2 para determinarmos a pressão no ponto1 e, finalmente, chegarmos a velocidade nesse ponto. Para isso, faremos uso dos pontos 3 e 4. Temos então:
\mathrm{{p_3} - {p_1} = {\gamma _a} \cdot h}
p3
−p1
=γa
⋅h
\mathrm{{p_4} - {p_3} = - {\gamma _m} \cdot 0,2}
p4
−p3
=−γm
⋅0,2
\mathrm{{p_2} - {p_4} = - {\gamma _a} \cdot \left( {h - 0,2} \right)}
p2
−p4
=−γa
⋅(h−0,2)
Logo, temos que:
\mathrm{{p_2} - {p_1} = - 0,2 \cdot \left( {{\gamma _m} - {\gamma _a}} \right)}
p2
−p1
=−0,2⋅(γm
−γa
)
Como foram dados que p2 é 20 kPa, \mathrm{\gamma _a}
γa
é 10 kN/m³ e \mathrm{\gamma _m}
γm
é 70 kN/m³, temos:
\mathrm{{p_1} = 32 kPa}
p1
=32kPa
Então, voltando para formulação encontrada no início da questão, temos:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{3,2 \cdot {{10}^4}}}{{10 \cdot {{10}^3}}} = 3,60m}
2⋅g
v1
2
+10⋅103
3,2⋅104
=3,60m
\mathrm{v_1^2 = 0,4 \cdot 2 \cdot 10}
v1
2
=0,4⋅2⋅10
\mathrm{{v_1} = 2,83m/s}
v1
=2,83m/s
Logo, a vazão do escoamento será:
\mathrm{Q = {v_1} \cdot A}
Q=v1
⋅A
\mathrm{Q = 2,83 \cdot 400 \cdot {10^{ - 4}}}
Q=2,83⋅400⋅10−4
\mathbf{Q = 0,1132{m^3}/s}
Q=0,1132m3
/s
Exercício 3
De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de 1,0 mH2O. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto S do sifão deve ser maior que – 60 kPa em pressão relativa e desprezando as perdas de carga determine a velocidade do fluido no sifão e a máxima altura que o ponto S pode ter em relação ao ponto A.
ESQUEMA DO EXERCÍCIO 1
Resolução
Para a resolução da questão, vamos inicialmente determinar a velocidade de fluxo no sifão.
Sabendo que a velocidade de escoamento em todo o sifão é a mesma, podemos utilizar a equação de Bernoulli entre os pontos A e B para determinar tal velocidade. Temos então que:
\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma }}
zA
+2⋅g
vA
2
+γ
pA
=zB
+2⋅g
vB
2
+γ
pB
Como temos que a pressão em ambos os pontos é a própria pressão atmosférica e que a velocidade no ponto A é nula, temos:
\mathrm{{z_A} = \dfrac{{v_B^2}}{{2 \cdot g}}}
zA
=2⋅g
vB
2
\mathbf{{v_B} = 5,66m/s}
vB
=5,66m/s
Agora que já temos o valor da velocidade do fluxo no sifão, podemos aplicar a equação de Bernoulli entre os pontos A e S.
Como temos que a pressão mínima no ponto S é -60 kPa e considerando agora o plano horizontal de referência passando pelo ponto A, temos:
\mathrm{0 = {z_S} + \dfrac{{5,{{66}^2}}}{{2 \cdot g}} - \dfrac{{60 \cdot {{10}^3}}}{{{{10}^4}}}}
0=zS
+2⋅g
5,662
−104
60⋅103
\mathbf{{z_S} = 4,4m}
zS
=4,4m
Exercício 2
Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:
- \mathrm{\gamma _a}
- γa
- : 10 kN/m³;
- \mathrm{\gamma _m}
- γm
- : 70 kN/m³;
- A: 400 cm²;
- p2: 20 kPa;
- g: 10 m/s².
ESQUEMA DO EXERCÍCIO 2
Resolução
Inicialmente, iremos demarcar na figura os pontos notáveis que iremos utilizar durante a questão para mais fácil entendimento no decorrer da mesma.
Os pontos foram escolhidos por serem pontos de mudança de fluido (água e fluido manométrico) ou por serem pontos que se sabe características como velocidade e pressão.
Logo, temos o seguinte esquema:
ESQUEMA PARA RESOLUÇÃO DO EXERCÍCIO 2
A questão pede que se determine a vazão do escoamento, ou seja, precisamos determinar a velocidade de escoamento.
Então, vamos aplicar a equação de Bernoulli para os pontos 1 e 5 do escoamento. Temos:
\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = {z_5} + \dfrac{{v_5^2}}{{2 \cdot g}} + \dfrac{{{p_5}}}{{{\gamma _a}}}}
z1
+2⋅g
v1
2
+γa
p1
=z5
+2⋅g
v5
2
+γa
p5
Como o ponto 5 possui velocidade nula, nele atua somente a pressão atmosférica e ele encontra-se numa cota 3,60 m acima do ponto 1, podemos desenvolver a equação para:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
Como não temos os valores de v1 e nem de p1, não conseguimos desenvolver, por ora, tal equacionamento.
Porém, temos um tubo U entre os pontos 1 e 2 e foi dada a pressão no ponto 2, então, podemos utilizar a lei de Stevin entre os pontos 1 e 2 para determinarmos a pressão no ponto1 e, finalmente, chegarmos a velocidade nesse ponto. Para isso, faremos uso dos pontos 3 e 4. Temos então:
\mathrm{{p_3} - {p_1} = {\gamma _a} \cdot h}
p3
−p1
=γa
⋅h
\mathrm{{p_4} - {p_3} = - {\gamma _m} \cdot 0,2}
p4
−p3
=−γm
⋅0,2
\mathrm{{p_2} - {p_4} = - {\gamma _a} \cdot \left( {h - 0,2} \right)}
p2
−p4
=−γa
⋅(h−0,2)
Logo, temos que:
\mathrm{{p_2} - {p_1} = - 0,2 \cdot \left( {{\gamma _m} - {\gamma _a}} \right)}
p2
−p1
=−0,2⋅(γm
−γa
)
Como foram dados que p2 é 20 kPa, \mathrm{\gamma _a}
γa
é 10 kN/m³ e \mathrm{\gamma _m}
γm
é 70 kN/m³, temos:
\mathrm{{p_1} = 32 kPa}
p1
=32kPa
Então, voltando para formulação encontrada no início da questão, temos:
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}
2⋅g
v1
2
+γa
p1
=3,60m
\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{3,2 \cdot {{10}^4}}}{{10 \cdot {{10}^3}}} = 3,60m}
2⋅g
v1
2
+10⋅103
3,2⋅104
=3,60m
\mathrm{v_1^2 = 0,4 \cdot 2 \cdot 10}
v1
2
=0,4⋅2⋅10
\mathrm{{v_1} = 2,83m/s}
v1
=2,83m/s
Logo, a vazão do escoamento será:
\mathrm{Q = {v_1} \cdot A}
Q=v1
⋅A
\mathrm{Q = 2,83 \cdot 400 \cdot {10^{ - 4}}}
Q=2,83⋅400⋅10−4
\mathbf{Q = 0,1132{m^3}/s}
Q=0,1132m3
/s
Exercício 3
De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de 1,0 mH2O. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Como calcular a tensão de cisalhamento na parede de um tubo e na região central?
Fenômenos de Transporte I
•UNB
Estudante PD
Quem é o atual capitão da seleção brasileira de futebol? (Preciso de pontos)
Fenômenos de Transporte I
•UNIP
Santos Domingos Pedro






Compartilhar