4. Encontre a área entre as curvas y = x2 e y = 2x. Quest.: 4 4/3 ua 3/4 ua 1 ua 2/3 ua 1/6 ua
💡 1 Resposta
Mateus Gonzalez
A região de integração está dada pela interseção das curvas, ou seja: \(0 \leq x \leq 2\). Para calcular a área temos:
\(\begin{eqnarray*} \int_{0}^{2} (2x-x^2)dx &=& x^2-\frac{x^3}{3} \Bigg|_{0}^{2} \\ &=& 4 - 8/3 \\ &=& 4/3 \end{eqnarray*}\)
RD Resoluções
Primeiro, deve-se encontrar os valores de \(x\) que delimitam a área entre as curvas \(y=x^2\) e \(2x\). Esses valores são:
\(\Longrightarrow x^2 = 2x\) \(\to \left \{ \begin{matrix} x_1 = 0 \\ x_2 = 2 \end{matrix} \right.\)
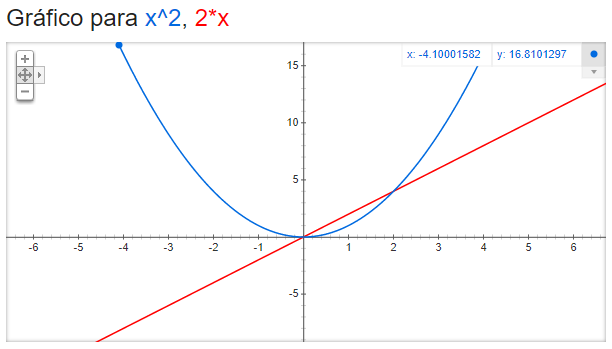
O gráfico das duas curvas está na figura a seguir:
Portanto, a área \(A\) entre as curvas é:
\(\Longrightarrow A = \int \limits_{x_1}^{x_2}(2x-x^2) \, dx\)
\(\Longrightarrow A = \int \limits_{0}^{2}(2x-x^2) \, dx\)
\(\Longrightarrow A =(x^2-{1 \over 3}x^3) \bigg |_0^2\)
\(\Longrightarrow A =(2^2-{1 \over 3}2^3) - (0^2-{1 \over 3}0^3) \)
\(\Longrightarrow A =(4-{8 \over 3}) - (0)\)
\(\Longrightarrow A ={4 \over 3} \)
Resposta correta: \(\fbox {$ {4 \over 3} $}\)
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta




Compartilhar