Como calcular distribuição contínua?

??

A variável aleatória considerada neste exemplo e muitas outras variáveis da área biológica podem ser descritas pelo modelo normal ou Gaussiano.

A equação da curva Normal é especificada usando 2 parâmetros: a média 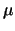, e o desvio padrão .

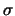Denotamos N(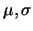) à curva Normal com média  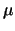e desvio padrão .

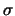A média refere-se ao centro da distribuição e o desvio padrão ao espalhamento (ou achatamento) da curva.

A distribuição normal é simétrica em torno da média o que implica que e média, a mediana e a moda são todas coincidentes.

Para referência, a equação da curva é 

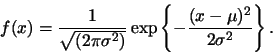
A área sob a curva normal (na verdade abaixo de qualquer função de densidade de probabilidade) é 1. Então, para quaisquer dois valores específicos podemos determinar a proporção de área sob a curva entre esses dois valores.

Para a distribuição Normal, a proporção de valores caindo dentro de um, dois, ou três desvios padrão da média são:

Range	Proportion
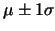	68.3%
	95.5%
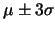	99.7%