Força Px

Conceitos

---

Para responder esta questão, é necessário revisarmos decomposição vetorial.

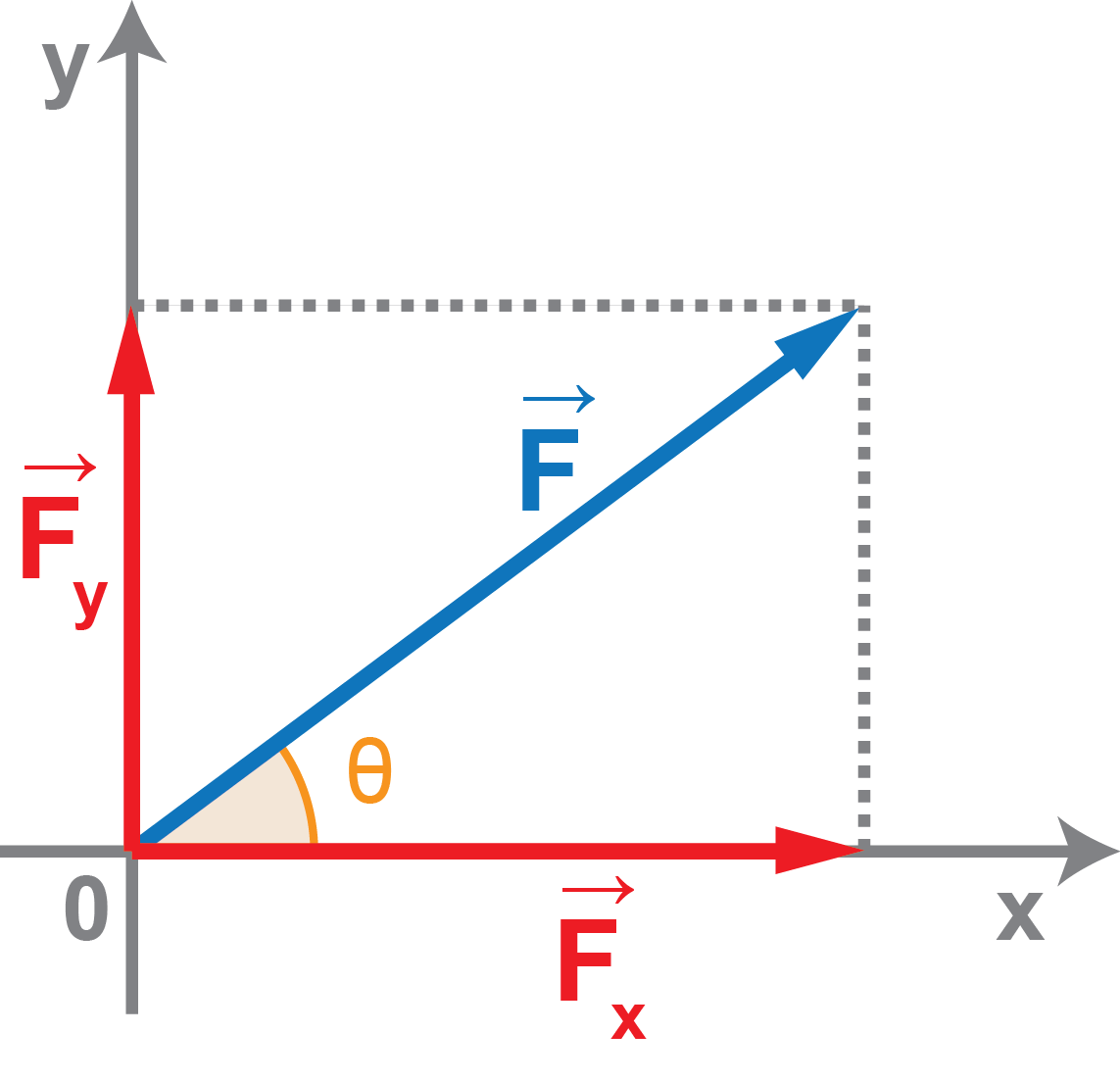
Sendo \(\vec{F}\) um vetor, podemos decompor as componentes de \(\vec{F}\) com relação à um sistema de eixos coordenados, através do ângulo \(\theta\) que o vetor faz com o eixo horizontal.

Resolução

---

Admitindo que exista um ângulo \(\theta\) não nulo entre o eixo horizontal \((x)\) e a força aplicada pelo dinamômetro \((FD)\), podemos decompor as componentes da força segundo os eixos vertical \((FD_y)\)e horizontal \((FD_x)\). Esta decomposição é visualizada geometricamente por um triângulo retângulo, em cuja geometria pode-se aplicar o teorema de Pitágoras, de forma que:

\(FD^2 = (FD_x)^2+(FD_y)^2\)

Sendo \((FD_x)\) a componente peso e \((FD)\) a força no dinamômetro, obtemos:

\(\begin{align} (0,87)^2 &= (0,85)^2+(FD_y)^2\\ (FD_y)^2 &= (0,87)^2 - (0,85)^2 \\ (FD_y)^2 &= 0,7569 - 0,7225 \\ (FD_y)^2 &= 0,0344 \\ (FD_y) &= 0,19N \\ \end{align}\)

---

Observamos que é possível o dinamômetro apresentar leitura maior que as componentes do peso próprio com relação aos eixos coordenados, uma vez que a força do dinamômetro corresponde à hipotenusa do triângulo retângulo de catetos correspondentes às componentes deste vetor.