Indique a função que é solução da equação diferencial y" - 4y' + 4y = ex.

yy

Muitas vezes, para resolver uma equação diferencial ordinária (EDO) de segunda ordem é preferível realizar uma substituição de variável e assim reduzir a ordem da EDO de 2 pra 1. Caso a EDO reduzida seja exata, pode-se usar o método de separação de variáveis, coso contrário, pode-se utilizar o método do fator integrante.

Iremos realizar uma substituição de variáveis da seguinte forma:

Assim, a nossa EDO fica da seguinte forma:

Reescreveremos a EDO assim:

A equação acima não é exata. Logo, multiplicaremos pelo fator integrante μ(y):

Denotaremos a parte que acompanha dz como M e a parte que acompanha dy como N, e encontraremos My e Nz, i.e., derivada parcial de M em relação à y e derivada parcial de N em relação à z. Assim, iremos forçar que a EDO se torne exata.

Para calcular My, faremos o seguinte:

Para calcular Nz, faremos o seguinte:

Igualando My e Nz, temos que:

Rearranjando os termos e integrando dos dois lados:

Pronto! Encontramos o fator integrante μ(y). Podemos substituí-lo na EDO e substituir o lado esquerdo da equação que é a derivada de um produto.

Integrando dos dois lados, temos:

Resolvendo a segunda integral do lado direito da equação pelo método da integração por partes, temos:

Portanto:

Mas z = y', então há mais uma última integral a ser feita. Rearranjando a equação e calculando sua integral, obtemos:

Portanto, através de algumas manipulações algébricas, conseguimos obter a solução de uma EDO de segunda ordem. A solução final é:

Onde K é uma constante arbitrária.

Muitas vezes, para resolver uma equação diferencial ordinária (EDO) de segunda ordem é preferível realizar uma substituição de variável e assim reduzir a ordem da EDO de 2 pra 1. Caso a EDO reduzida seja exata, pode-se usar o método de separação de variáveis, coso contrário, pode-se utilizar o método do fator integrante.

Iremos realizar uma substituição de variáveis da seguinte forma:

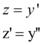
Assim, a nossa EDO fica da seguinte forma:

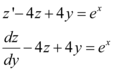
Reescreveremos a EDO assim:

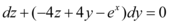
A equação acima não é exata. Logo, multiplicaremos pelo fator integrante μ(y):

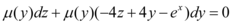
Denotaremos a parte que acompanha dz como M e a parte que acompanha dy como N, e encontraremos My e Nz, i.e., derivada parcial de M em relação à y e derivada parcial de N em relação à z. Assim, iremos forçar que a EDO se torne exata.

Para calcular My, faremos o seguinte:

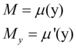
Para calcular Nz, faremos o seguinte:

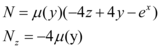
Igualando My e Nz, temos que:

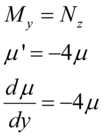
Rearranjando os termos e integrando dos dois lados:

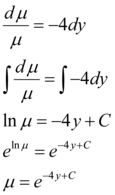
Pronto! Encontramos o fator integrante μ(y). Podemos substituí-lo na EDO e substituir o lado esquerdo da equação que é a derivada de um produto.

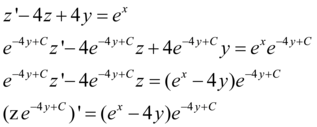
Integrando dos dois lados, temos:

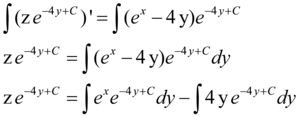
Resolvendo a segunda integral do lado direito da equação pelo método da integração por partes, temos:

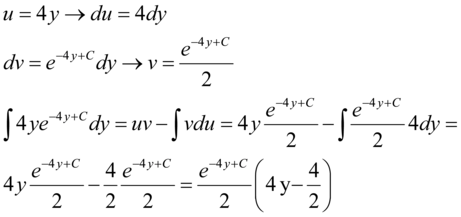
Portanto:

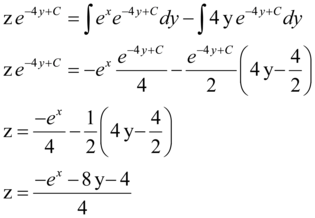
Mas z = y', então há mais uma última integral a ser feita. Rearranjando a equação e calculando sua integral, obtemos:

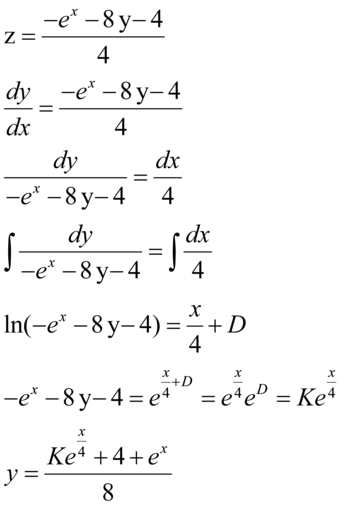
Portanto, através de algumas manipulações algébricas, conseguimos obter a solução de uma EDO de segunda ordem. A solução final é:

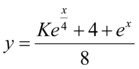
Onde K é uma constante arbitrária.