) Suponha que a taxa de crescimento é substituída pelo seu valor médio 1/10. Determine o tempo de duplicação τ nesse caso.
💡 4 Respostas
Marcelino Marcos Arruda Silva
Muito boa pergunta
Andre Smaira
Neste exercício, será calculado o tempo de duplicação  de uma população qualquer.
de uma população qualquer.
Será considerado um valor inicial 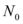 de uma população que cresce a uma taxa de valor médio
de uma população que cresce a uma taxa de valor médio  ao longo do tempo (que pode ser em segundos, minutos, horas...). Portanto, pós um tempo
ao longo do tempo (que pode ser em segundos, minutos, horas...). Portanto, pós um tempo  , a equação da quantidade dessa população é:
, a equação da quantidade dessa população é:
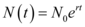
Pelo enunciado, tem-se que 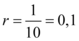 . Portanto, a equação anterior fica da seguinte forma:
. Portanto, a equação anterior fica da seguinte forma:
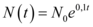
No instante  , a quantidade da população é o dobro da inicial, ou seja,
, a quantidade da população é o dobro da inicial, ou seja, 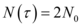 . Substituindo
. Substituindo  na equação anterior, tem-se o seguinte:
na equação anterior, tem-se o seguinte:
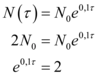
Portanto, o valor de  é:
é:
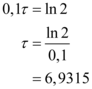
Concluindo, o tempo de duplicação, em unidades de tempo, de uma população é:
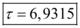
Andre Smaira
Neste exercício, será calculado o tempo de duplicação de uma população qualquer.
Será considerado um valor inicial de uma população que cresce a uma taxa de valor médio
ao longo do tempo (que pode ser em segundos, minutos, horas...). Portanto, pós um tempo
, a equação da quantidade dessa população é:
Pelo enunciado, tem-se que . Portanto, a equação anterior fica da seguinte forma:
No instante , a quantidade da população é o dobro da inicial, ou seja,
. Substituindo
na equação anterior, tem-se o seguinte:
Portanto, o valor de é:
Concluindo, o tempo de duplicação, em unidades de tempo, de uma população é:
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Qual é a taxa anual efectiva que permite a duplicação de um capitaal no prazo de 42 meses?
Calculo Financeiro
•SIN SIGLA
Nery Amador
Materiais relacionados
 3 pág.
3 pág. 5 pág.
5 pág. 1 pág.
1 pág.




Compartilhar