Buscar

Taxas relacionadas.

Um avião voa horizontalmente a uma atitude de 2 km ,a 800 km/h,  e passa diretamente  sobre uma estação de radar. Encontre a taxa segundo a qual a distância entre o avião e a estação aumentea quando ele esa a 3 km aém da estação.

Cálculo I

•

ESTÁCIO

0
Dislike0
0
Dislike0
Reply2
User badge image

Rodrigo Cézar Oliveira

💡 2 Respostas

User badge image

Suzana Costa

Imagine um triângulo retângulo. Chamaremos o cateto oposto ao angulo de x, o adjacente de z representando a altura do avião e valendo 2, e por último a hipotenusa, que chamaremos de y, onde representa a distância entre o avião e a estação. Aplicando Pitágoras, obtemos:

y^{2}=x^{2}+2^{2} \\ \\ \\ y^{2} = x^{2}+4

Derivando cada termo e adotando as notações em função do tempo, temos:

\displaystyle y^{2} = x^{2} + 4 \\ \\ \\ 2y \, \frac{dy}{dt} = 2x \, \frac{dx}{dt}

Temos que isolar a notação dy/dt que representa a variação da hipotenusa e simplesmente, a variação da distância entre o avião e a estação:

\displaystyle 2y \, \frac{dy}{dt} = 2x \, \frac{dx}{dt} \\ \\ \\ \frac{dy}{dt} = \frac{2x}{2y} \, \frac{dx}{dt} \\ \\ \\ \frac{dy}{dt} = \frac{x}{y} \, \frac{dx}{dt}

Perceba que se y² = x² + 4, então:

x = \sqrt{y^2-4}

Então temos:

\displaystyle \frac{dy}{dt} = \frac{x}{y} \, \frac{dx}{dt} \\ \\ \\ \frac{dy}{dt} = \frac{\sqrt{y^{2}-4}}{y} \, \frac{dx}{dt}

Considere as informações dadas:

\displaystyle \frac{dx}{dt}=800 \, km/h \\ \\ \\ y=3 \, km \\ \\ \\ \frac{dy}{dt}= \, ?

Substituindo esses valores na expressão, temos a seguinte resposta para o problema:

\displaystyle \frac{dy}{dt} = \frac{\sqrt{y^{2}-4}}{y} \, \frac{dx}{dt} \\ \\ \\ \frac{dy}{dt} = \frac{\sqrt{3^{2}-4}}{3} \cdot 800 \\ \\ \\ \boxed{\boxed{\frac{dy}{dt} = \frac{800\sqrt{5}}{3} \, km/h}}

0
Dislike0
User badge image

RD Resoluções

Para resolver este problema devemos colocar em prática nossos conhecimentos sobre taxas relacionadas.

Inicialmente, deve-se relacionar a posição do avião com a localização da estação, que pode ser definida como um vetor posição ( ), contendo duas componentes horizontal (x) e vertical (y)

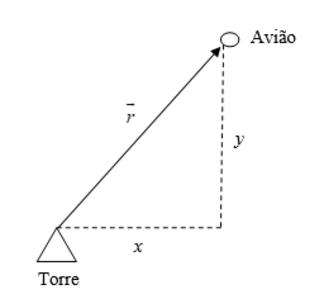
Além disso, distância entre a torre e o avião pode ser encontrada por meio do módulo do vetor posição. 

Para encontrar a taxa em que a distância entre o avião e a torre aumenta basta derivar o módulo do vetor posição em relação ao tempo:

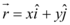
Derivando implicitamente, tem-se:

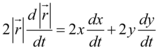
em que   é a velocidade horizontal, 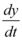  é a velocidade vertical e  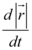 é a taxa de variação da distância entre a torre e o avião. Portanto, 

0
Dislike0

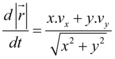
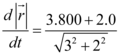
✏️ Responder

SetasNegritoItálicoSublinhadoTachadoCitaçãoCódigoLista numeradaLista com marcadoresSubscritoSobrescritoDiminuir recuoAumentar recuoCor da fonteCor de fundoAlinhamentoLimparInserir linkImagemFórmula

Para escrever sua resposta aqui, entre ou crie uma conta

User badge image

Outros materiais

Outros materiais