como calcular o limite infinito na equação

https://www.somatematica.com.br/superior/limites/limites4.php

Olá!

Calcular o limite quando este tende ao infinito depende de análises simplesmente. São 3 os casos mais comuns:

1) Pede-se +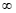 ou -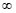 em um polinômio. Repare que + 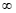é o mesmo que colocar um número muito grande no polinômio, e este vai resultar em um número muito grande. Logo este limite resultará em +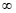. Se for pedido o limite tendendo a - 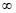fique atento aos graus dos polinômios, pois, polinômios pares farão a potência se tornar positiva, se ímpares, estes se tornarão negativos. Desta forma estes polinômios com x tendendo a - 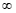podem ter duas respostas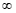, ou + ou -.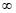

2) Pede-se para calcular o limite tendendo a +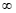 ou -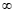 em uma razão. Repare que um número dividido por um número muito grande tenderá a zero, tanto se este positivo, como se este for negativo. Desta maneira, se a função no denominador tender a + 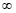ou -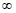, esta deverá ir para zero. Atenção, pois o numerador neste caso deve ser um valor constante, ou independente.

3) o numerador e o denominador são dependentes de x tender a +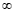 ou -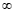. Neste caso você deverá aplicar a regra de L'Hopital, e em seguida, observar se ocorre o caso 1 ou 2 aqui mostrados.

E é isto!

Bons estudos!