Verifique se as transformações a seguir são lineares:? T: R² --> R², T(x,y)= (3y-x, y-x).
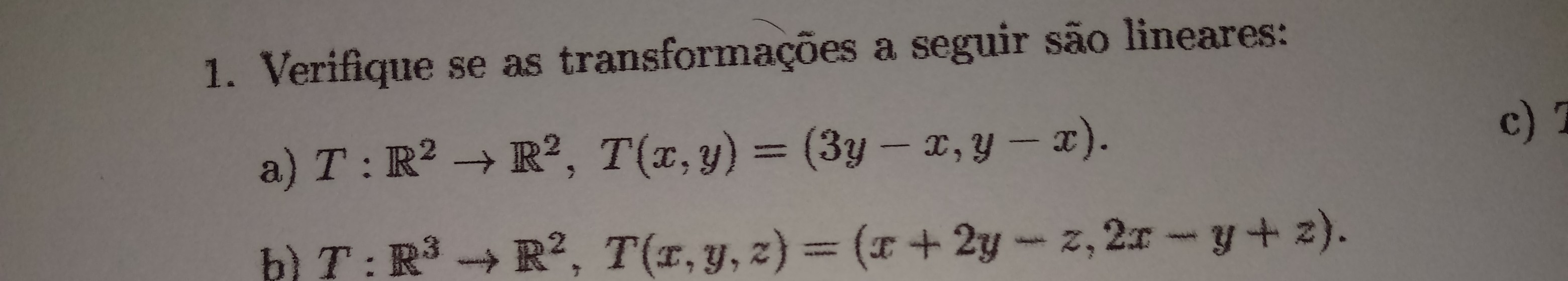
💡 7 Respostas
Rafael Trindade Miranda
a) T : R² → R² , definida por T( x , y ) = ( x - y , 0 )
Neste caso não basta só verificar T( 0 , 0 ) = 0, temos que aplicar a definição, vem;
Devemos mostrar que :
l - T( u + v ) = T( u ) + F( v ) ; ∀u = ( x₁ , y₁ ) e v = ( x₂ , y₂ ) ∈ ℝ²
T( u + v ) = T( ( x₁ , y₁ ) + ( x₂ , y₂ ) ) = T( x₁ + x₂ , y₁ + y₂ ) = ( x₁ + x₂ - y₁ - y₂ , 0 )
T( u + v ) = ( x₁ - y₁ , 0 ) + ( x₂ - y₂ , 0 ) = T( x₁ , y₁ ) + T( x₂ , y₂ )
T( u + v ) = T( u ) + T( v )
A primeira condição é satisfeita!
ll - T( αu ) = αT( u ) , ∀u = ( x₁ , y₁ ) ∈ ℝ² e ∀α ∈ ℝ²
T( αu ) = αT( u )
T( αu ) = T( α( x₁ , y₁ ) ) = T( αx₁ , αy₁ ) = ( αx₁ - αy₁ , 0 ) = ( α.( x₁ - y₁ ) , 0 ) = α.( x₁ - y₁ , 0 ) = αT( x₁ , y₁ )
T( αu ) = αT( u ).
A segunda condição também é satisfeita!
R ────────► Portanto, T é uma transformação linear.
Oliveira Alves502
Andre Smaira
---
Uma transformação \(T\) é dita linear quando dados os elementos \(u\) e \(v\) e o escalar \(\alpha\) são válidas as seguintes relações:
- \(T(u+v)=T(u)+T(v)\)
- \(T(\alpha u)=\alpha T(u)\)
---
Vamos verificar essas relações para o nosso caso, tomando \(u=(x_u,y_u)\) e \(v=(x_v,y_v)\). É dado:
\[T(x,y)=(3y-x,y-x)\]
Para a primeira propriedade, temos:
\[T(u+v)=T(x_u+x_v,y_u+y_v)=(3(y_u+y_v)-(x_u+x_v),(y_u+y_v)-(x_u+x_v))\]
Usando a propriedade distributiva, temos:
\[T(u+v)=(3y_u+3y_v-x_u-x_v,y_u+y_v-x_u-x_v)\]
Rearranjando:
\[T(u+v)=((3y_u-x_u)+(3y_v-x_v),(y_u-x_u)+(y_v-x_v))\]
Separando como uma soma de vetores, temos:
\[T(u+v)=(3y_u-x_u,y_u-x_u)+(3y_v-x_v,y_v-x_v)\]
Ou:
\[\boxed{T(u+v)=T(u)+T(v)}\]
---
Vamos agora verificar a segunda propriedade:
\[T(\alpha u)=T(\alpha x_u,\alpha y_u)=(3(\alpha y_u)-(\alpha x_u),(\alpha y_u)-(\alpha x_u))\]
Fatorando com o fator \(\alpha\) comum em evidência:
\[T(\alpha u)=(\alpha (3y_u-x_u),\alpha (y_u- x_u))\]
Evidenciando \(\alpha\) também em relação ao vetor:
\[T(\alpha u)=\alpha(3y_u-x_u,y_u- x_u)\]
Logo:
\[\boxed{T(\alpha u)=\alpha T(u)}\]
------
Concluímos, portanto, que a transformação a seguir é uma transformação linear:
\[\boxed{T(x,y)= (3y-x, y-x)}\]
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
determine se são transformações lineares T: R² → R²: Questão a) T(x,y) = (x + 2y, xy) Questão b) T(x,y) = (x + 2y, 0)
Algebra Linear e Estrutura Algebrica
•IFRJ
Nathan Nascimento







Compartilhar