Dúvida sobre o Teorema de Green

\[\int\int_S \bigg( {\partial Q \over \partial x} - {\partial P \over \partial y} \bigg ) \partial x \partial y \,\,\,\, (I)\]

----

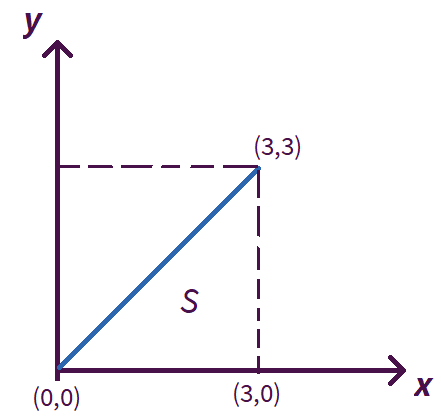
1. Determinação da área \(S\): a área \(S\) é descrita pelo seguinte trecho: “sobre a região limitada pelo triângulo de vértices: (0,0), (3,0) e (3,3).”

Colocando esses pontos no eixo cartesiano, tem-se o seguinte:

1558048638788

----

É possível perceber que a reta azul (que liga os vértices \((0,0)\) e \((3,3)\) no gráfico) consiste na função \(y=x\). Com isso, a região \(S\) pode ser escrita da seguinte forma:

\[S=\{(x,y) \in \mathbb{R}:0 \le x \le 3, \, 0 \le y \le x\}\]

----

1. Campo \(\overrightarrow{F}(x,y)=(x+y)\hat{i}-(x^2+y^2)\hat{j}\): o campo está no formato \(\overrightarrow{F}(x,y)=P\hat{i}+Q\hat{j}\). Portanto, as funções \(P\) e \(Q\) são:


\[\left\{ \begin{matrix} P=x+y \\ Q=-(x^2+y^2) =-x^2-y^2 \end{matrix} \right.\]


----

1. Cálculo da circulação-rotacional: com bases nas considerações anteriores, a integral \((I)\) fica da seguinte forma:


\[\begin{align} \int\int_S \bigg( {\partial Q \over \partial x} - {\partial P \over \partial y} \bigg ) \partial x \partial y &= \int_0^3 \int_0^x \bigg[ {\partial (-x^2-y^2) \over \partial x} - {\partial (x+y) \over \partial y} \bigg ] \partial y \partial x \\ &= \int_0^3 \int_0^x \bigg[ (-2x) - (1) \bigg ] \partial y \partial x \\ &= \int_0^3 \int_0^x \bigg[ -2x -1 \bigg ] \partial y \partial x \\ \end{align}\]


----

Integrando em \(\partial y\), tem-se o seguinte:


\[\begin{align} \int\int_S \bigg( {\partial Q \over \partial x} - {\partial P \over \partial y} \bigg ) \partial x \partial y &= \int_0^3 \Bigg\{ \int_0^x \bigg[ -2x -1 \bigg ] \partial y \Bigg\} \partial x \\ &= \int_0^3 \Bigg\{ \bigg[ -2x -1 \bigg ] y \Big|_0^x \Bigg\} \partial x \\ &= \int_0^3 \Bigg\{ \bigg[ -2x -1 \bigg ] x \Bigg\} \partial x \\ \end{align}\]


---

Integrando em \(\partial x\), o resultado final é:


\[\begin{align} \int\int_S \bigg( {\partial Q \over \partial x} - {\partial P \over \partial y} \bigg ) \partial x \partial y &= \int_0^3 \bigg[ -2x -1 \bigg ] x \, \partial x \\ &= \int_0^3 \bigg[ -2x^2 -x \bigg ] \partial x \\ &= \bigg[ -{2 \over 3}x^3 -{1 \over 2}x^2 \bigg ] \bigg|_0^3 \\ &= \bigg[ -{2 \over 3}(3)^3 -{1 \over 2}(3)^2 \bigg ]-\bigg[ -{2 \over 3}(0)^3 -{1 \over 2}(0)^2 \bigg ] \\ &= \bigg[ -18 -4,5 \bigg ]-\bigg[ 0 \bigg ] \\ &= -22,5 \end{align}\]


Resposta correta: letra a) -22,5.

----

Concluindo, pelo Teorema de Green, a circulação-rotacional de um dado campo vetorial é a alternativa \(\boxed{\text{a)} -22,5}\).

12,5

FIZ DUAS VEZES DEU A MESMA RESPOSTAS