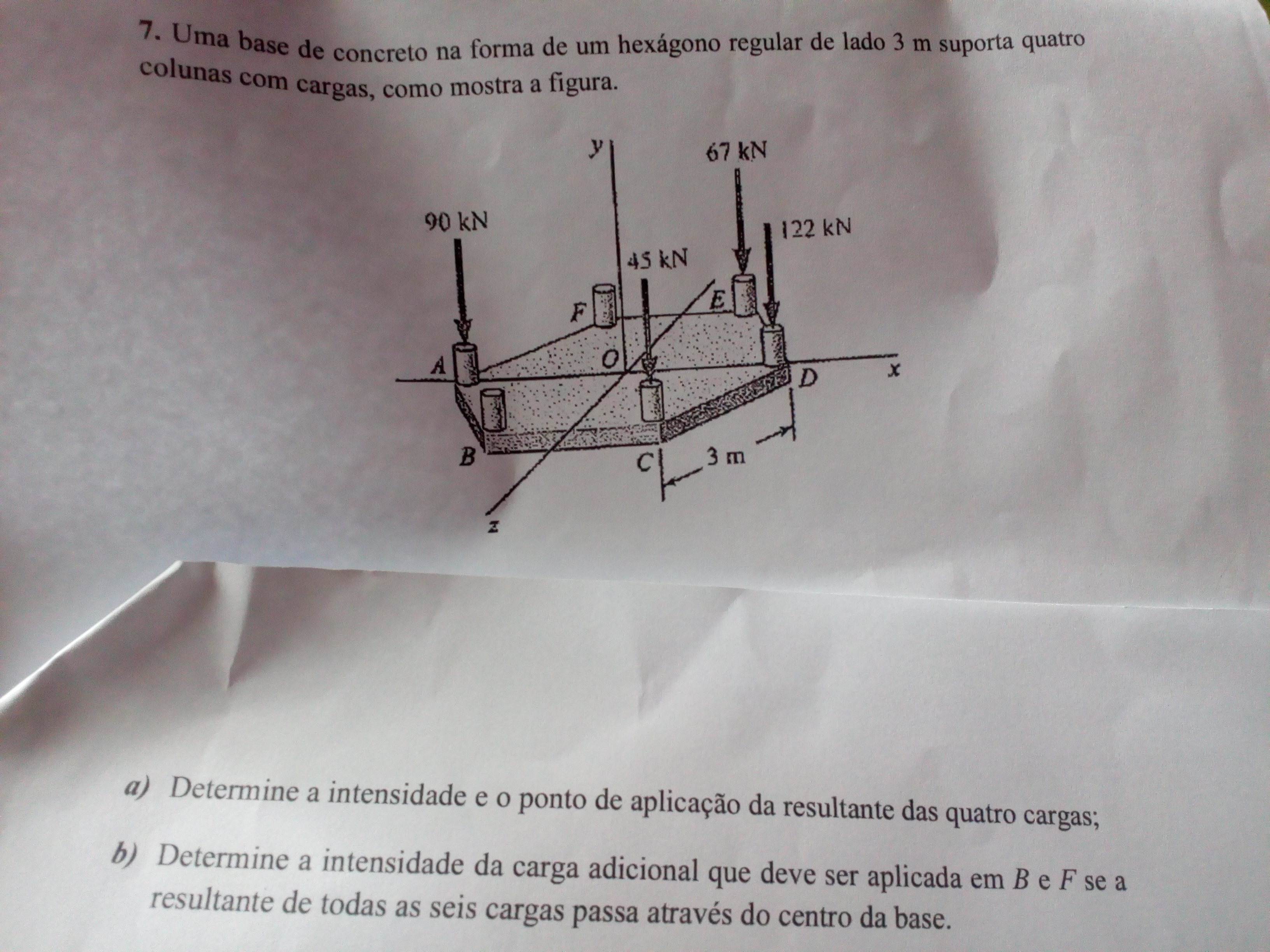
Uma placa de concreto na forma de um hexágono retangular de lado 3 m suporta quatro colunas com cargas, como mostra a figura. Responda?

a) A intensidade da resultante das cargas será:

67 +  122 + 45 + 90 = 324kN

O ponto de aplicação da resultante será aquele que produz o mesmo momento sobre a placa, em relação aos eixos coordenados:

Momento em relação ao eixo z:

90.3k - 122.3k - 67.1,5k - 45.1,5k = - 324.x

270 - 366 - 100,5 - 67,5 = - 324.x

-264 = -324x

x =  0,845 m

Momento em relação ao eixo x:

67.2,6 - 45.2,6 = 324z

z = 0,177 m

Então o ponto de aplicação da força será:

P = (0,845 ; 0 ; 0,177) 

b) Para que a resultante passar pelo centro da base os momentos em relação aos eixos x, y e z devem ser nulos, deve-se atribuir uma variável tipo Fb e Ff e montar um sistema de duas equações e duas icógnitas, assim chega-se a intensidade das forças.

A intensidade da resultante será dada por:

\[\eqalign{ & R = 67 + 122 + 45 + 90 \cr & R = 324{{\ kN}} }\]

Já o ponto de aplicação será:

\[\eqalign{ & {{para\ }}z: \cr & \cr & 90 \cdot 3 - 122 \cdot 3 - 67 \cdot 1,5 - 45 \cdot 1,5 = 324 \cdot x \cr & 270 - 366 - 100,5 - 67,5 = 324x \cr & x = 0,84{{\ m}} \cr & \cr & {{para\ }}x: \cr & \cr & 67 \cdot 2,6 - 45 \cdot 2,6 = 324z \cr & z = 0,18{{\ m}} }\]

Portanto, o ponto de aplicação será de \(\boxed{P = \left( {0,84;0,18} \right)}\).

b)

Para que a força resultante esteja aplicada no centro da base devemos ter momentos em relação aos eixos x, y e z de valor igual a zero, o que consequentemente fará com que seja necessário montar um sistema com uma variável tipo Fb e Ff para encontrarmos a intensidade das forças.