Qual as naturezas das cargas e a massa m da esfera de carga Q2?
|
|
||
 |
||
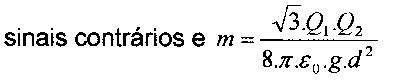 |
||
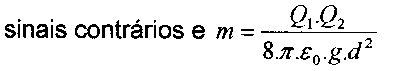 |
||
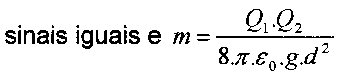 |
||
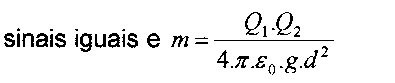 |
💡 5 Respostas
Junior Souza
questão incompleta
Andre Smaira
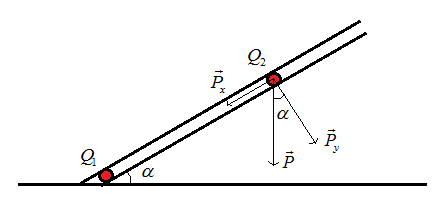
Autoria Própria
---
Para que a esfera de carga \({Q_2}\) fique em equilíbrio, deve existir uma força \({\vec F}\), de natureza elétrica, que anule a componente \({{\vec P}_x}\). Logo, essa força deve ter a mesma direção, a mesma intensidade e sentido contrário ao da componente mencionada. Para que isso, ocorra, as esferas devem se repelir. Ou seja, suas cargas devem ter sinais iguais.
---
Assim, a força \({\vec F}\) pode ser determinada pela lei de Coulomb que diz que a força eletrostática entre dois corpos é proporcional ao produto de suas cargas e inversamente proporcional ao quadrado da distância que os separa. O fator de proporcionalidade é dado por \(\dfrac{1}{{4\pi {\varepsilon _0}}}\), onde \({{\varepsilon _0}}\) é a permissividade do vácuo. Logo, para a sua intensidade, temos:
\[F = \dfrac{1}{{4\pi {\varepsilon _0}}} \cdot \dfrac{{{Q_1} \cdot {Q_2}}}{{{d^2}}}\]
---
Para determinar a intensidade da componente \({{\vec P}_x}\), vamos utilizar o triângulo retângulo formado pelos vetores \({{\vec P}_x}\), \({{\vec P}_y}\) e \({\vec P}\) na figura anterior. Assim, por meio das relações trigonométricas, podemos escrever:
\[\eqalign{ \dfrac{{{P_x}}}{P} &= \sin \alpha\cr{P_x} &= P \cdot \sin \alpha\cr&= mg \cdot \sin 30^\circ\cr&= \dfrac{{mg}}{2} }\]
---
Igualando as intensidades de \(F\) e \({P_x}\), temos:
\[\eqalign{ \dfrac{1}{{4\pi {\varepsilon _0}}} \cdot \dfrac{{{Q_1} \cdot {Q_2}}}{{{d^2}}} &= \dfrac{{mg}}{2}\crm &= \dfrac{{2 \cdot {Q_1} \cdot {Q_2}}}{{4 \cdot \pi \cdot {\varepsilon _0} \cdot g \cdot {d^2}}}\cr&= \dfrac{{{Q_1} \cdot {Q_2}}}{{2 \cdot \pi \cdot {\varepsilon _0} \cdot g \cdot {d^2}}} }\]
---
Portanto, como os sinais devem ser iguais e a massa é \(\boxed{m = \dfrac{{{Q_1} \cdot {Q_2}}}{{2 \cdot \pi \cdot {\varepsilon _0} \cdot g \cdot {d^2}}}}\), deve ter algum erro de digitação das alternativas.
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Materiais relacionados
 1 pág.
1 pág. 1 pág.
1 pág.





Compartilhar