(UERJ 2017) Considere a circunferência C de equação x2 + y2 − 8x + 8 = 0, representada graficamente a seguir.
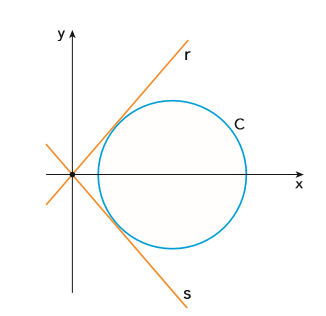
Determine as equações das retas r e s que passam pela origem e são tangentes à circunferência.
💡 2 Respostas
Bruno Coutinho
Profª. Thayná Leal (matemática)
Equação da reta r: mr*x , note que mr > 0
Como é tangente à circunferência, temos que
x² + (mrx)² - 8x + 8 = 0
x²(1+(mr)²) - 8x + 8 = 0
Resolvendo usando delta (deverá ser igual a zero), temos:
Δ = 64 - 4*(1+(mr)²)*8 = 0
0 = 64 -4(8+8(mr)²)
0 = 64 -32 - 32(mr)²
mr = 1
Logo, a equação da reta será : 1x = x
Note que ms < 0
Logo, a equação será s: - x
Faça como milhares de estudantes: teste grátis o Passei Direto
Esse e outros conteúdos desbloqueados
16 milhões de materiais de várias disciplinas
Impressão de materiais
Agora você pode testar o
Passei Direto grátis
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Compartilhar