Resistência dos Materiais I A junta está sujeita a uma força de 1,25 kN, como mostra a figura. Determine a tensão nos pontos C e B
A junta está sujeita a uma força de 1,25 kN, como mostra a figura. Determine a tensão nos pontos C e B
se a seção transversal retangular do elemento tiver largura de 12 mm e espessura de 18 mm.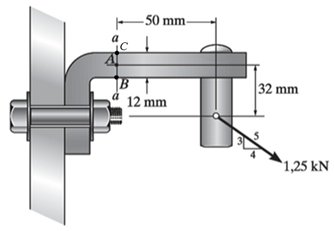
| A | σC=17,36 MPa e σB=−8,10MPa | ||||
| B |
| ||||
| C | σC=15,20 MPa e σB=6,3MPa |
| |||
| D | σC=8,80 MPa e σB=−14,20MPa |
|
Respostas
Andre Smaira
há 6 anos
Sabendo que a área da seção transversal é \(A=216\;mm^2\), podemos calculas a tensão de tração que atua em todos os pontos do elemento, \(\sigma_t=\dfrac FA=\dfrac{1000}{216}=4,63\;N/mm^2\).
A flexão pela força vertical causará tração na parte de cima do elemento e compressão na parte de baixo, sendo a tensão causada \(\sigma_f=\dfrac{Fly}{I_x}\), sendo \(l=50\;mm\) a distância da aplicação da força aos pontos analisados, \(y\) a coordenada vertical do ponto analisado e \(I_x=\dfrac{bh^3}{12}=\dfrac{18\cdot12^3}{12}=2592\;mm^4\). Para o ponto \(C\), \(y=6\;mm\), assim, \(\sigma_{fC}=86,8\; N/mm^2\). Já para o ponto \(B\), \(y=-6\;mm\), assim, \(\sigma_{fB}=-86,8\; N/mm^2\).
Já a flexão pela força horizontal causará tração na parte de baixo do elemento e compressão na parte de cima, sendo a tensão causada \(\sigma_{fx}=-\dfrac{Fhx}{I_x}\), sendo \(h=32\;mm\) a distância da aplicação da força aos pontos analisados, \(y\) a coordenada vertical do ponto analisado e \(I_x=\dfrac{bh^3}{12}=\dfrac{18\cdot12^3}{12}=2592\;mm^4\). Para o ponto \(C\), \(y=6\;mm\), assim, \(\sigma_{fC}=-74,1\; N/mm^2\). Já para o ponto \(B\), \(y=-6\;mm\), assim, \(\sigma_{fB}=+74,1\; N/mm^2\).
Assim, encontramos \(\boxed{\sigma_B=-8,1\;MPa}\) e \(\boxed{\sigma_C=17,3\;MPa}\).
Portanto, a alternativa correta é a letra (A).


Crie sua conta grátis para liberar essa resposta. 🤩
Já tem uma conta?
Ao continuar, você aceita os Termos de Uso e Política de Privacidade
Debora Casao
há 5 anos
resposta: (A) c=17,36 MPa e B=-8,10MPA
Willian Silva
há 6 anos





