Obter as equações simétricas da reta r que passa pelo ponto A(-1,0,-1) e que intercepta as retas r1 e r2.
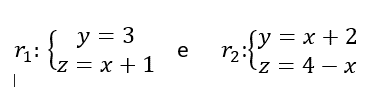
💡 1 Resposta
Ghylherme Patriota
Seja:
r1(x1) = (y(x1),z(x1)) = (3, 1+x1)
r2(x2) = (y(x2), z(x2)) = (x2+2, 4-x2). Devemos encontrar o ponto onde elas se interceptam:
r1 = r2 ====> (3, 1+x1) = (x2+2, 4-x2). Temos o sistema:
3 = x2+2 ===> x2=1
1+x1 = 4-x2 ====> x1+x2 = 3, logo x1 = 2, dado que x2 = 1;
Portanto se interceptam no ponto r1(2) = (3,3) = r2(1) = (3,3);
Peguemos como vetor diretor da reta r o vetor que passa por (3,3) e (-1,0,-1) = A. Temos:
(3,3,0) - (-1,0,-1) = (4,3,1).
Agora seja r(t) = (3,3,0) + t(4,3,1), onde r(0) é no ponto (3,3,0) = (3,3) e r(-1) = A. Sendo assim:
x = 3+4t ===> t = (x-3)/4
y = 3+3t ===> t = (y-3)/3
z = t
Portanto nossa equações simétricas de r são:
(x-3)/4 = (y-3)/3 = z;
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Estabeleça as equações simétricas da reta r que passa pelo ponto A(2, 1,−4) e B(3, 2,−2) ?
Geometria Analítica e Álgebra Linear
•UFRA
davidtata
As equações simétricas da reta r que contem o ponto P=(−1,3,5) e é perpendicular ao plano π:x−y+2z−1=0 são: a. x+11=y−3−1=z−52 b. x+11=y−31=z−5...
Geometria Analítica e Álgebra Linear
•UNINGÁ
Ana Maria Sanches hipolito
Determinar as equações simétricas da reta que é simultaneamente perpendicular as retas
Geometria Analítica
•UNIFRAN
igor gomes
Materiais relacionados
 3 pág.
3 pág.




Compartilhar