Como fazer essa questão de GA (cônicas)?
O movimento de satelites e espac¸ onaves no espac¸ o est ´ a sujeito a forc¸ a de atrac¸ ´ ao gravi- ˜ tacional dos corpos celestes que induz trajetorias descritas por curvas/sec¸ ´ oes c ˜ onicas. Por ˆ exemplo, uma missao espacial designada para estudar certo planeta, parti da terra reali- ˜ zando uma trajetoria parab ´ olica tendo tal planeta como foco. Este percurso possibilita que ´ a espac¸ onave se aproxime do planeta para coletar imagens da superficie e ao mesmo tempo ainda utilizada a forc¸ a da gravidade para impulsionar o movimento sem que haja gastos de energia/combust´ıvel.
Quando a espac¸ onave esta a ´ 5.107 km do planeta investigado, sabemos que o segmento de reta que os conecta forma um angulo de ˆ π 3 (ou 60o grau) com o eixo da parabola. Determine a menor dist ´ ancia entre estes durante tal trajet ˆ oria para que sejam ´ tiradas as melhores imagens do planeta em questao. ˜ Questao 2. ˜ Tendo em vista que tal planeta esta localizado nas coordenadas P = (0, 5.103 ), encontre a equac¸ao da trajet ˜ oria parab ´ olica e determine todos os principais elementos ´ desta curva.
💡 4 Respostas
wemerson ricardo peixoto dazilio
NAO SEI
Andre Smaira
Quando a espaçonave está a 5.107 km do planeta investigado, sabemos que o segmento de reta que os conecta forma um angulo de π/3 (ou 60o) com o eixo da parábola. Determine a menor distância entre estes durante tal trajetória para que sejam tiradas as melhores imagens do planeta em questão. ˜ Questão 2. ˜ Tendo em vista que tal planeta está localizado nas coordenadas P = (0, 5.103 ), encontre a equação da trajetória parabólica e determine todos os principais elementos desta curva.
Nesse exercício vamos estudar o conceito de parábola e suas propriedades.
Nosso problema é descrito pela seguinte imagem:
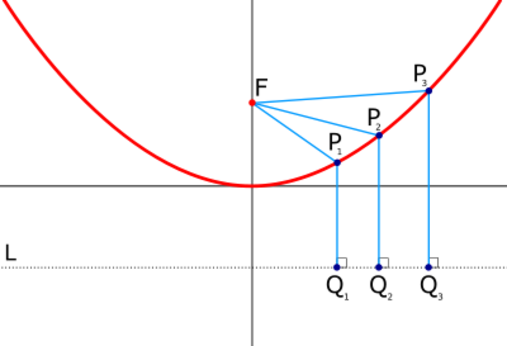
Fonte: https://pir2.forumeiros.com/t37166-parabola
É importante lembrar a definição de parábola: curva formada pelos pontos que equidistam do foco $F$ e da diretriz. Tomemos o ponto estudado como o ponto $P_1$ da imagem. A menor distância entre a espaçonave e o planeta acontece quando ela passa pelo vértice da parábola. Podemos escrever a distância entre o foco e a diretriz de duas formas:
$$d_{F,d}=d_{F,V}+ d_{V,d}=d_{F,P}\cos\theta+d_{P,d}$$
Substituindo nossos dados, temos:
$$2d_{F,V}=5107\cos60^o+5107=7660,5\Rightarrow\boxed{d_{F,V}=3830,25\ km}$$
Sabendo que o planeta está localizado em $F=(0;5103)$, vamos determinar a equação da parábola e seus principais elementos. Para isso novamente vamos usar a definição:
$$d_{X,F}=y+d_{F,V}\Rightarrow \sqrt{x^2+(y-y_F)^2}=y+y_F$$
Elevando ao quadrado, temos:
$$x^2+(y^2-2yy_F+y_F^2)=y^2+2y y_F + y_F^2$$
Simplificando:
$$x^2-2yy_F=2y y_F\Rightarrow y = {1\over4y_F}x^2\Rightarrow \boxed{y={x^2\over15321}}$$
O foco da parábola é a posição do planeta:
$$\boxed{F=(0;5103)}$$
E a diretriz:
$$\boxed{y_d=-5103}$$
Andre Smaira
Quando a espaçonave está a 5.107 km do planeta investigado, sabemos que o segmento de reta que os conecta forma um angulo de π/3 (ou 60o) com o eixo da parábola. Determine a menor distância entre estes durante tal trajetória para que sejam tiradas as melhores imagens do planeta em questão. ˜ Questão 2. ˜ Tendo em vista que tal planeta está localizado nas coordenadas P = (0, 5.103 ), encontre a equação da trajetória parabólica e determine todos os principais elementos desta curva.
Nesse exercício vamos estudar o conceito de parábola e suas propriedades.
Nosso problema é descrito pela seguinte imagem:
Fonte: https://pir2.forumeiros.com/t37166-parabola
É importante lembrar a definição de parábola: curva formada pelos pontos que equidistam do foco $F$ e da diretriz. Tomemos o ponto estudado como o ponto $P_1$ da imagem. A menor distância entre a espaçonave e o planeta acontece quando ela passa pelo vértice da parábola. Podemos escrever a distância entre o foco e a diretriz de duas formas:
$$d_{F,d}=d_{F,V}+ d_{V,d}=d_{F,P}\cos\theta+d_{P,d}$$
Substituindo nossos dados, temos:
$$2d_{F,V}=5107\cos60^o+5107=7660,5\Rightarrow\boxed{d_{F,V}=3830,25\ km}$$
Sabendo que o planeta está localizado em $F=(0;5103)$, vamos determinar a equação da parábola e seus principais elementos. Para isso novamente vamos usar a definição:
$$d_{X,F}=y+d_{F,V}\Rightarrow \sqrt{x^2+(y-y_F)^2}=y+y_F$$
Elevando ao quadrado, temos:
$$x^2+(y^2-2yy_F+y_F^2)=y^2+2y y_F + y_F^2$$
Simplificando:
$$x^2-2yy_F=2y y_F\Rightarrow y = {1\over4y_F}x^2\Rightarrow \boxed{y={x^2\over15321}}$$
O foco da parábola é a posição do planeta:
$$\boxed{F=(0;5103)}$$
E a diretriz:
$$\boxed{y_d=-5103}$$
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Não entendi como fazer essa questão de GA, alguem poderia me ajudar ?
Geometria Analítica
•IFSC
Lênin Paulo Michelon
Como fazer gráfico de superfícies( cilindricas,cônicas e de revolução) e quádricas?
Geometria Analítica
•UNICAMP
Estudante PD







Compartilhar