Encontre o domínio da função:
A) f(x) = x + 4 / x² - 9
B) f (x) = 2x³ - 5 / x² + x - 6
C) ³ √2t - 1
D) √3 - t - √2+t
E) 1 / ⁴√x² - 5x
💡 4 Respostas
Lindomar Schvambach
A) (X Є R | X ≠ -3 e X ≠ 3)
B) (X Є R | X ≠ -3 e X ≠ 2)
C) Todos os reais.
D) [ -2 ≤ X ≤ 3 ]
E) Todos os reais.
Laysa Samara
A) D={x∈R|x≠3,-3}, pois se x for 3 o denominador irá zerar.
B) D={x∈R|x≠2,-3}, se resolvermos, encontramos os valores de x que fazem a função definida. Para assíntotas e pontos de descontinuidades é mais fácil encontrar onde a expressao não é definida. Portanntao os valores encontrados não farão parte do domínio.
C) D={x∈R}
D) D={x∈R}
E) D={x∈R|x≠0,1/25}, 0, pois, o deominador não pode zerar e 1/25 encontramos quando igualamos o denominador a 0 assim como na alternamtiva B e encontramos onde a função não é definida.
Andre Smaira
O domínio de uma função nos permite identificar quais valores a variável pode assumir. Sendo assim, vamos analisar cada equação para encontrar o seu domínio.
No ítem A, temos uma razão, onde o numerador é um polinômio do primeiro grau e o denominador é um polinômio do segundo grau. O domínio dos polinômios são o conjunto dos números reais portanto não há nenhuma restrição para eles. Mas em uma razão o denominador não pode assumir o número zero. Sendo assim:
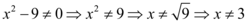
O domínio então é os números reais com x diferente de 3: 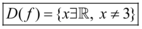
No ítem B, a mesma regra da razão do ítem A deve ser aplicada. Assim, temos:
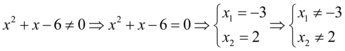
Assim, o domínio da função é: 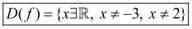
No ítem C, temos uma raíz do terceiro grau com o argumento sendo um polinômio do primeiro grau. O argumento de uma raíz não pode ser menor que zero. Sendo assim:
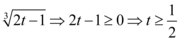
O domínio da função é: 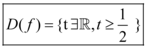
No ítem D temos duas raízes quadradas. E a mesma regra do ítem C para raízes é válida, o seu argumento não deve ser menor que zero:
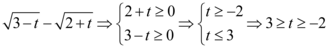
O domínio da função é: 
No ítem E temos uma razão e raíz a quarta com um polinômio de segundo grau como argumento. Para o polinômio não há uma regra mas para a raíz é válida a mesma regra do ítem C. E para a razão, seu denominador deve ser diferente de zero. Sendo assim:
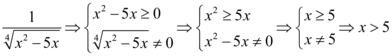
O domínio da função é: 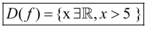
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta





Compartilhar