Sabendo que as retas r e s são ortogonais, determine o valor de m

Primeiramente vamos organizar as duas retas e encontrar dois vetores, cada um pertencente a uma delas:

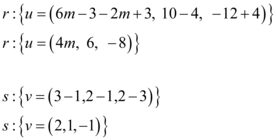
Como elas são ortogonais, o produto entre os vetores deve ser igual a 0. Sendo assim temos:

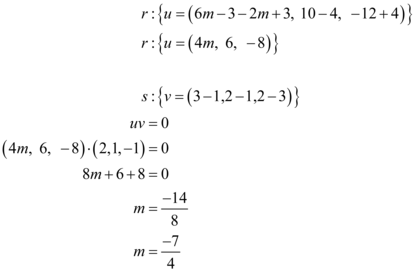
Portanto, o valor de m será  . 

dsdddddddddffdggfffgfff

Para que duas retas sejam ortogonais, seus vetores diretores devem ser ortogonais. Então, primeiramente vamos determinar os vetores diretores de \(r\) e \(s\). 

• Para \(r\) temos que o vetor diretor é \(\vec{v_r}=(2m,3,-4)\).
• Para \(s\) temos que o vetor diretor é \(\vec{v_s}=(2,1,-1)\).

Desta forma, para que os vetores diretores sejam ortogonais, o produto escalar entre eles deve ser nulo, ou seja,

\(\vec{v_r}\cdot\vec{v_s}=0\Longleftrightarrow4m+3+4=0\Longleftrightarrow4m=-7\Longleftrightarrow m=-\frac{7}{4}.\)