algebra linear
Leia o excerto de texto a seguir: 1.
Para determinarmos se um conjunto de vetores é L.I. ou L.D. devemos fazer a combinação linear do
conjunto de vetores e igualar esta combinação linear ao vetor nulo do espaço”.
Após essa avaliação, caso queira ler o texto integralmente, ele está disponível em:
http://www.joinville.udesc.br/portal/professores/katiani/materiais/apostila_2011.pdf>. Acesso em 22 fev
2018.
Com base no fragmento do texto acima e nos conteúdos do livro-base Álgebra Linear e dados os vetores
= (1, 2 , 5), v 2 = (4, 5, -1) e v 3 = (2,3,2), verifique:
se os vetores são linearmente independentes ou dependentes em .
se vetores formam uma base. Em caso afirmativo, determine as coordenadas de , em
relação aos vetores
Justifique a tua resposta em cada item.
R
3
v = (11, 13, −11)
v 1 , v 2 , v 3 .
💡 3 Respostas
RD Resoluções
Foram utilizados conhecimentos em álgebra linear para resolver a questão.
Para verificar se os vetores são LD ou LI, fazemos o seguinte processo:
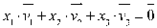
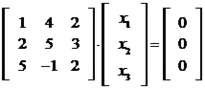
Devemos agora escalonar a matriz dos coeficientes. Fazendo os seguinte pivotamento,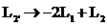 
e 
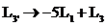, temos
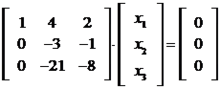
Continuando o escalonamento, faremos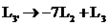 
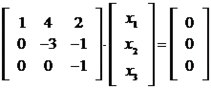
Resolvendo o sistema, vemos que a única solução possível é a trivial, ou seja:
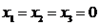
Portanto, os vetores são linearmente independentes.
Para que os vetores formem uma base, eles precisam ser LI, fato que já foi provado anteriormente e tem que ser capaz de gerar todos os vetores do espaço vetorial, ou seja:
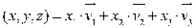
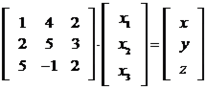
Realizando os mesmos pivotamentos do caso anterior, temos que:
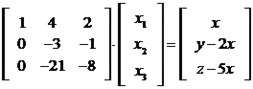
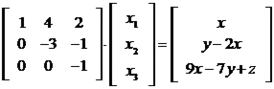
Agora podemos calcular os valore d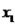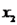e 
, 
e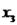 
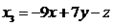
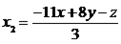
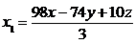
Desta forma, podemos inferir que todo vetor do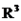 
pode ser escrito de forma única em relação a 
, 
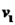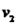e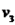 
.
Desta maneira, satisfeitas as duas condições para ser uma base, podemos afirmar que os três vetores,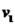 
, 
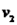e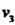 
, são base do espaço vetorial 
.
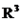Para calcular as coordenadas do vetor em uma dada base, faremos da seguinte maneira:
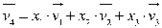
Ond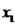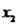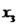e 
, 
, 
e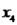 
são as coordenadas do vetor em questão na nossa base. Da parte anterior da resolução, temos que:
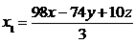
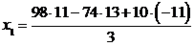
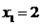
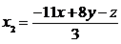
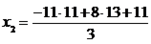
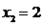
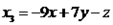
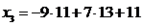
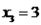
Portanto, as coordenadas do vetor na base dada é
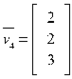
https://www.ime.unicamp.br/~marcia/AlgebraLinear/Arquivos%20PDF/exemplos_base.pdf -acessado dia 11/10/18
Andre Smaira
Foram utilizados conhecimentos em álgebra linear para resolver a questão.
Para verificar se os vetores são LD ou LI, fazemos o seguinte processo:
Devemos agora escalonar a matriz dos coeficientes. Fazendo os seguinte pivotamento, 
e 
, temos
Continuando o escalonamento, faremos 
Resolvendo o sistema, vemos que a única solução possível é a trivial, ou seja:
Portanto, os vetores são linearmente independentes.
Para que os vetores formem uma base, eles precisam ser LI, fato que já foi provado anteriormente e tem que ser capaz de gerar todos os vetores do espaço vetorial, ou seja:
Realizando os mesmos pivotamentos do caso anterior, temos que:
Agora podemos calcular os valore de 
, 
e 
Desta forma, podemos inferir que todo vetor do 
pode ser escrito de forma única em relação a 
, 
e 
.
Desta maneira, satisfeitas as duas condições para ser uma base, podemos afirmar que os três vetores, 
, 
e 
, são base do espaço vetorial 
.
Para calcular as coordenadas do vetor em uma dada base, faremos da seguinte maneira:
Onde 
, 
, 
e 
são as coordenadas do vetor em questão na nossa base. Da parte anterior da resolução, temos que:
Portanto, as coordenadas do vetor na base dada é
https://www.ime.unicamp.br/~marcia/AlgebraLinear/Arquivos%20PDF/exemplos_base.pdf -acessado dia 11/10/18
Faça como milhares de estudantes: teste grátis o Passei Direto
Esse e outros conteúdos desbloqueados
16 milhões de materiais de várias disciplinas
Impressão de materiais
Agora você pode testar o
Passei Direto grátis
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Outros materiais
Perguntas relacionadas
Materiais relacionados
137 pág.
4 pág.
Compartilhar