matematica elementar
apresente pelo menos 3 exempols de funcao do 1 grau (completa e incompleta)encontre suas raizes ,represente graficamente e faca o estudo de sinal das mesmas.Obs:.Um dos exemplos deve ser do tipo problema ou situacao-problema,em outras palavras,uma aplicacao de funcaodo1 grau
💡 3 Respostas
Andre Smaira
Contextualização:
Consideremos x e y duas variáveis, sendo uma dependente da outra, isto é, para cada valor atribuído a x corresponde um valor para y. Definimos essa dependência como função, nesse caso, y está em função de x. O conjunto de valores conferidos a x deve ser chamado de domínio da função e os valores de y são a imagem da função.
Toda função é definida por uma lei de formação, no caso de uma função do 1º grau a lei de formação será a seguinte: 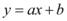 , onde a e b são números reais e
, onde a e b são números reais e  .
.
Esse tipo de função deve ser dos Reais para os Reais.
A representação gráfica de uma função do 1º grau é uma reta. Analisando a lei de formação 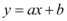 , notamos a dependência entre x e y, e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função é crescente ou decrescente e o valor de b indica o ponto de intersecção da função com o eixo y no plano cartesiano.
, notamos a dependência entre x e y, e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função é crescente ou decrescente e o valor de b indica o ponto de intersecção da função com o eixo y no plano cartesiano.
Referência:
Site https://mundoeducacao.bol.uol.com.br/matematica/funcao-1-grau.htm - Acessado em 04/10/2018
Site https://brasilescola.uol.com.br/matematica/aplicacoes-uma-funcao-1-grau.htm - Acessado em 04/10/2018
Resolução:
Exemplos de funções do 1º grau:
1) 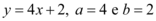
Para encontrar as raízes: 
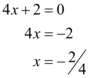
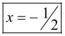
A reta representada pela função 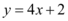 intersecta o eixo x no seguinte valor: –1/2
intersecta o eixo x no seguinte valor: –1/2
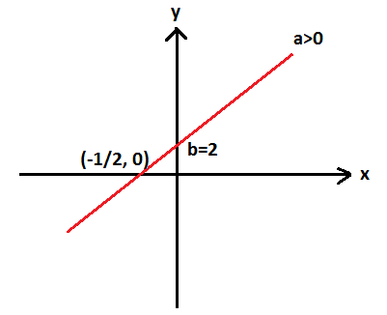
2) 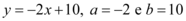
Para encontrar as raízes: 
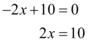

A reta representada pela função 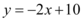 intersecta o eixo x no seguinte valor: 5
intersecta o eixo x no seguinte valor: 5
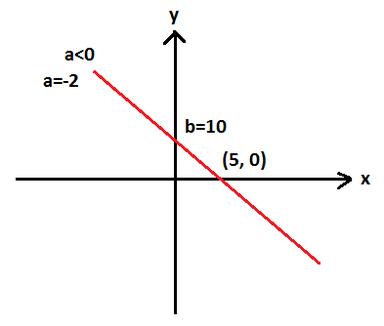
3) Situação-Problema
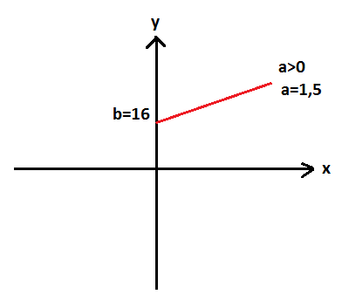
Na produção de peças, uma fábrica tem um custo fixo de R$ 16,00 mais um custo variável de R$ 1,50 por unidade produzida. Sendo x o número de peças unitárias produzidas, o custo pode ser calculado através da equação abaixo:
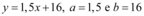
Como o mínimo de peças produzidas é zero, o custo fixo mínimo é de 16, quando  .
.
Conclusão:
Portanto, tendo em vista que toda função é definida por uma lei de formação, e no caso de uma função do 1º grau a lei de formação é: 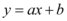 , onde a e b são números reais e
, onde a e b são números reais e  .
.
A representação gráfica de uma função do 1º grau é uma reta. Analisando a lei de formação 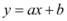 , notamos a dependência entre x e y, e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função é crescente ou decrescente e o valor de b indica o ponto de intersecção da função com o eixo y no plano cartesiano.
, notamos a dependência entre x e y, e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função é crescente ou decrescente e o valor de b indica o ponto de intersecção da função com o eixo y no plano cartesiano.
Andre Smaira
Contextualização:
Consideremos x e y duas variáveis, sendo uma dependente da outra, isto é, para cada valor atribuído a x corresponde um valor para y. Definimos essa dependência como função, nesse caso, y está em função de x. O conjunto de valores conferidos a x deve ser chamado de domínio da função e os valores de y são a imagem da função.
Toda função é definida por uma lei de formação, no caso de uma função do 1º grau a lei de formação será a seguinte: , onde a e b são números reais e
.
Esse tipo de função deve ser dos Reais para os Reais.
A representação gráfica de uma função do 1º grau é uma reta. Analisando a lei de formação , notamos a dependência entre x e y, e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função é crescente ou decrescente e o valor de b indica o ponto de intersecção da função com o eixo y no plano cartesiano.
Referência:
Site https://mundoeducacao.bol.uol.com.br/matematica/funcao-1-grau.htm - Acessado em 04/10/2018
Site https://brasilescola.uol.com.br/matematica/aplicacoes-uma-funcao-1-grau.htm - Acessado em 04/10/2018
Resolução:
Exemplos de funções do 1º grau:
1)
Para encontrar as raízes:
A reta representada pela função intersecta o eixo x no seguinte valor: –1/2
2)
Para encontrar as raízes:
A reta representada pela função intersecta o eixo x no seguinte valor: 5
3) Situação-Problema
Na produção de peças, uma fábrica tem um custo fixo de R$ 16,00 mais um custo variável de R$ 1,50 por unidade produzida. Sendo x o número de peças unitárias produzidas, o custo pode ser calculado através da equação abaixo:
Como o mínimo de peças produzidas é zero, o custo fixo mínimo é de 16, quando .
Conclusão:
Portanto, tendo em vista que toda função é definida por uma lei de formação, e no caso de uma função do 1º grau a lei de formação é: , onde a e b são números reais e
.
A representação gráfica de uma função do 1º grau é uma reta. Analisando a lei de formação , notamos a dependência entre x e y, e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função é crescente ou decrescente e o valor de b indica o ponto de intersecção da função com o eixo y no plano cartesiano.
RD Resoluções
Contextualização:
Consideremos x e y duas variáveis, sendo uma dependente da outra, isto é, para cada valor atribuído a x corresponde um valor para y. Definimos essa dependência como função, nesse caso, y está em função de x. O conjunto de valores conferidos a x deve ser chamado de domínio da função e os valores de y são a imagem da função.
Toda função é definida por uma lei de formação, no caso de uma função do 1º grau a lei de formação será a seguinte: , onde a e b são números reais e
.
Esse tipo de função deve ser dos Reais para os Reais.
A representação gráfica de uma função do 1º grau é uma reta. Analisando a lei de formação , notamos a dependência entre x e y, e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função é crescente ou decrescente e o valor de b indica o ponto de intersecção da função com o eixo y no plano cartesiano.
Referência:
Site https://mundoeducacao.bol.uol.com.br/matematica/funcao-1-grau.htm - Acessado em 04/10/2018
Site https://brasilescola.uol.com.br/matematica/aplicacoes-uma-funcao-1-grau.htm - Acessado em 04/10/2018
Resolução:
Exemplos de funções do 1º grau:
1)
Para encontrar as raízes:
A reta representada pela função intersecta o eixo x no seguinte valor: –1/2
2)
Para encontrar as raízes:
A reta representada pela função intersecta o eixo x no seguinte valor: 5
3) Situação-Problema
Na produção de peças, uma fábrica tem um custo fixo de R$ 16,00 mais um custo variável de R$ 1,50 por unidade produzida. Sendo x o número de peças unitárias produzidas, o custo pode ser calculado através da equação abaixo:
Como o mínimo de peças produzidas é zero, o custo fixo mínimo é de 16, quando .
Conclusão:
Portanto, tendo em vista que toda função é definida por uma lei de formação, e no caso de uma função do 1º grau a lei de formação é: , onde a e b são números reais e
.
A representação gráfica de uma função do 1º grau é uma reta. Analisando a lei de formação , notamos a dependência entre x e y, e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função é crescente ou decrescente e o valor de b indica o ponto de intersecção da função com o eixo y no plano cartesiano.
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta







Compartilhar