Um vaso de pressão cilíndrico com diâmetro externo de 900 mm é construído enrolando, no formato de uma espiral, uma placa de aço
com 15 mm de espessura e fixando as bordas adjacentes por meio de uma solda de topo. As costuras da solda de topo formam um ângulo de 30° com um plano transversal através do cilindro. Determine a tensão normal σ perpendicular à solda quando a pressão interna do vaso for de 2,2 MPa.
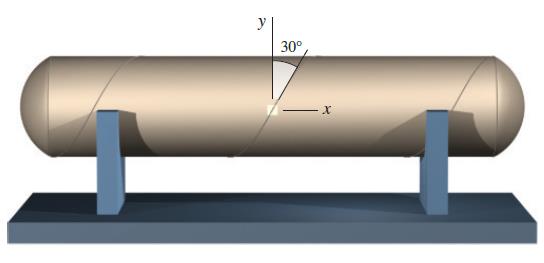
Assinale a alternativa correta.
Alternativas
Alternativa 1:
35,8 MPa.
Alternativa 2:
36,7 MPa.
Alternativa 3:
39,9 MPa.
Alternativa 4:
40,9 MPa.
Alternativa 5:
41,2 MPa.
💡 6 Respostas
Andre Smaira
\[\eqalign{ & {\sigma _T} = \dfrac{{Pd}}{{2t}} \cr & {\sigma _T} = 63,8{\text{ MPa}} \cr & {\sigma _L} = \dfrac{{Pd}}{{4t}} \cr & {\sigma _L} = 31,9{\text{ MPa}} }\]
----
Para encontrarmos a tensão cisalhante, realizaremos os seguintes cálculos:
\[\eqalign{ & \tau = 3\left( { - \left( {\sigma x - \sigma y} \right)\sin \theta \cos \theta + \tau xy\left( { - {{\sin }^2}\theta + {{\cos }^2}\theta } \right)} \right) \cr & \tau = - 3\left( {\left( {31,9 - 63,8} \right)\sin 30 \cdot \cos 30 + 0} \right) \cr & \tau = 41,2{\text{ MPa}} }\]
----
Portanto, a tensão cisalhante será de \(\boxed{\tau = 41,2{\text{ MPa}}}\).
Gilberto Yamakawa
Alternativa 3
39,9 MPa
Pablo Amorim
41,2mpa
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Um vaso de pressão cilíndrico com diâmetro externo de 900 mm, uma placa de aço com 15 mm de espessura, As costuras da solda formam um ângulo de 30°.
Resistência dos Materiais I
•UNICESUMAR EAD
Kaká Rayanne
Materiais relacionados
 1 pág.
1 pág. 1 pág.
1 pág.




Compartilhar