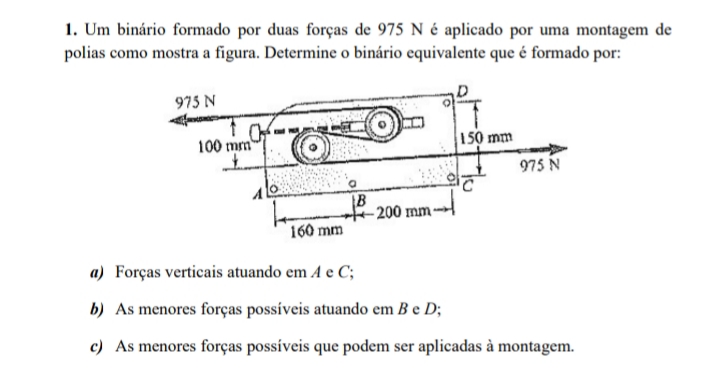
Um binário formando por duas forças de 975N.determine o binario equivale?

Acho que a resposta é:

a) O binário atuante das forças será 975 x 0.1 = 97.5 N.m

O binário resistente deverá ser igual, contudo com braço de 160mm + 200mm = 360 mm = 0.36m

Assim as forças em A e C serão, em módulo:

91.5 N.m = F x 0.36 m

FA = FC = 91.5 / 0.36 = 254.17 N

b) O binário atuante continua o mesmo 97.5N.m, contudo se fixarmos por B e D o braço será a hipotenusa do triângulo BCD temos:

Hbcd² = 0.2² + 0.15²   <> Hbcd = 0.25 m

FB = FD = 97.5 / 0.25 = 390 N

c) As menores forças possíveis surgem quando temos o maior braço, nesse caso a diagonal do triângulo ACD 

Hacd² = 0.36² + 0.15²  <>  Hacd = 0.39 m

FA = FD = 91.5/0.39 = 234.62 N

Sabendo que as forças estão configuradas como mostrado, a somatória dos momentos no ponto A será dada por:

\(M_a=975.0,1+975.0,05=146,25\)

O valor da força é dado pelo binário:

\(F_A=0\\ F_b={146,25 \over 0,16}=914,06\)